Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T07:10:59.290Z Has data issue: false hasContentIssue false
  • English
  • Français

On the approximation of algebraic numbers by algebraic integers

Published online by Cambridge University Press:  09 April 2009

K. Mahler
K. Mahler
Affiliation:
Institute of Advanced Studies, Australian National University, Canberra, A.C.T., 16 November, 1962.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In his Topics in Number Theory, vol. 2, chapter 2 (Reading, Mass., 1956) W. J. LeVeque proved an important generalisation of Roth's theorem (K. F. Roth, Mathematika 2,1955, 1—20).

Let ξ be a fixed algebraic number, σ a positive constant, and K an algebraic number field of degree n. For κ∈K denote by κ(1), …, κ(n) the conjugates of κ relative to K, by h(κ) the smallest positive integer such that the polynomial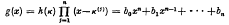 has rational integral coefficients, and by q(κ) the quantity

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 3 , Issue 4 , November 1963 , pp. 408 - 434
Copyright
Copyright © Australian Mathematical Society 1963