Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T07:21:45.789Z Has data issue: false hasContentIssue false
  • English
  • Français

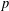ON SPRINDŽUK’S CLASSIFICATION OF $p$-ADIC NUMBERS

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  12 December 2019

YANN BUGEAUD  and
GÜLCAN KEKEÇ
YANN BUGEAUD
Affiliation:
Université de Strasbourg, CNRS, IRMA UMR 7501, 7, rue René Descartes, 67000Strasbourg, France e-mail: [email protected]
GÜLCAN KEKEÇ
Affiliation:
Istanbul University, Faculty of Science, Department of Mathematics, 34134Vezneciler, Istanbul, Turkey e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We carry Sprindžuk’s classification of the complex numbers to the field 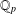$\mathbb{Q}_{p}$ of 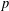$p$-adic numbers. We establish several estimates for the 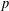$p$-adic distance between 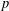$p$-adic roots of integer polynomials, which we apply to show that almost all 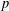$p$-adic numbers, with respect to the Haar measure, are 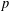$p$-adic 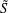$\tilde{S}$-numbers of order 1.

Keywords

Sprindžuk’s classification of the complex numbersp-adic transcendental numberstranscendence measureroots of an integer polynomial in ℂpLiouville’s inequality

MSC classification

Primary: 11J61: Approximation in non-Archimedean valuations
Secondary: 11J82: Measures of irrationality and of transcendence
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 2 , October 2021 , pp. 221 - 231
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by M. Coons

This research was supported by the Scientific Research Projects Coordination Unit of Istanbul University (project number FUA-2018-31152).

References

Amou, M., ‘On Sprindžuk’s classification of transcendental numbers’, J. reine angew. Math. 470 (1996), 27–50.Google Scholar
Amou, M., ‘Transcendence measures for almost all numbers’, in: Analytic Number Theory (Kyoto, 1995), Sũrikaisekikenkyũsho Kõkyũroku, 961 (1996), 112–116 (in Japanese).Google Scholar
Amou, M. and Bugeaud, Y., ‘Sur la séparation des racines des polynômes et une question de Sprindžuk’, Ramanujan J. 9 (2005), 25–32.CrossRefGoogle Scholar
Amou, M. and Bugeaud, Y., ‘On integer polynomials with multiple roots’, Mathematika 54 (2007), 83–92.CrossRefGoogle Scholar
Bugeaud, Y., Approximation by Algebraic Numbers, Cambridge Tracts in Mathematics, 160 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Chudnovsky, G. V., Contributions to the Theory of Transcendental Numbers, American Mathematical Society Surveys and Monographs, 19 (American Mathematical Society, Providence, RI, 1984).CrossRefGoogle Scholar
Diaz, G. and Mignotte, M., ‘Passage d’une mesure d’approximation à une mesure de transcendance’, C. R. Math. Rep. Acad. Sci. Canada 13 (1991), 131–134.Google Scholar
Mahler, K., ‘Zur Approximation der Exponentialfunktionen und des Logarithmus. I, II’, J. reine angew. Math. 166 (1932), 118–150.Google Scholar
Mahler, K., ‘Über eine Klasseneinteilung der p-adischen Zahlen’, Mathematica (Leiden) 3 (1935), 177–185.Google Scholar
Sprindžuk, V. G., ‘On a classification of transcendental numbers’, Litovsk. Mat. Sb. 2 (1962), 215–219 (in Russian).Google Scholar
Sprindžuk, V. G., Mahler’s Problem in Metric Number Theory (American Mathematical Society, Providence, RI, 1969).Google Scholar
Waldschmidt, M., Diophantine Approximation on Linear Algebraic Groups, Grundlehren der mathematischen Wissenschaft, 326 (Springer, Berlin–Heidelberg–New York, 2000).CrossRefGoogle Scholar