Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T08:49:30.190Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SEMIGROUPS WITH PSPACE-COMPLETE SUBPOWER MEMBERSHIP PROBLEM

Part of: Theory of computing Semigroups

Published online by Cambridge University Press:  30 May 2018

MARKUS STEINDL
MARKUS STEINDL*
Affiliation:
Institute for Algebra, Johannes Kepler University Linz, Altenberger St 69, 4040 Linz, Austria Department of Mathematics, University of Colorado Boulder, Campus Box 395, Boulder, CO 80309-0395, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

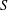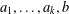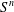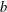Fix a finite semigroup $S$ and let $a_{1},\ldots ,a_{k},b$ be tuples in a direct power $S^{n}$. The subpower membership problem (SMP) for $S$ asks whether $b$ can be generated by 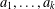$a_{1},\ldots ,a_{k}$. For combinatorial Rees matrix semigroups we establish a dichotomy result: if the corresponding matrix is of a certain form, then the SMP is in P; otherwise it is NP-complete. For combinatorial Rees matrix semigroups with adjoined identity, we obtain a trichotomy: the SMP is either in P, NP-complete, or PSPACE-complete. This result yields various semigroups with PSPACE-complete SMP including the six-element Brandt monoid, the full transformation semigroup on three or more letters, and semigroups of all $n$ by $n$ matrices over a field for 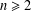$n\geq 2$.

Keywords

subalgebras of powersmembership testcomputational complexityPSPACE-completeNP-complete

MSC classification

Primary: 20M99: None of the above, but in this section
Secondary: 68Q25: Analysis of algorithms and problem complexity
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 106 , Issue 1 , February 2019 , pp. 127 - 142
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The author was supported by the Austrian Science Fund (FWF): P24285.

References

Bulatov, A., Kozik, M., Mayr, P. and Steindl, M., ‘The subpower membership problem for semigroups’, Internat. J. Algebra Comput. 26(07) (2016), 1435–1451.Google Scholar
Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups. Vol. I, Mathematical Surveys, 7 (American Mathematical Society, Providence, RI, 1961).Google Scholar
Cook., S. A., ‘Characterizations of pushdown machines in terms of time-bounded computers’, J. Assoc. Comput. Mach. 18 (1971), 4–18.Google Scholar
Howie, J. M., Fundamentals of Semigroup Theory, London Mathematical Society Monographs. New Series, 12 (The Clarendon Press, Oxford University Press, New York, Oxford Science Publications, 1995).Google Scholar
Idziak, P., Marković, P., McKenzie, R., Valeriote, M. and Willard, R., ‘Tractability and learnability arising from algebras with few subpowers’, SIAM J. Comput. 39(7) (2010), 3023–3037.Google Scholar
Kozen, D., ‘Complexity of finitely presented algebras’, in: Conference Record of the Ninth Annual ACM Symposium on Theory of Computing (Boulder, CO, 1977) (Association for Computing Machinery, 1977), 164–177.Google Scholar
Kozik., M., ‘A finite set of functions with an EXPTIME-complete composition problem’, Theoret. Comput. Sci. 407(1–3) (2008), 330–341.Google Scholar
Mayr, P., ‘The subpower membership problem for Mal’cev algebras’, Internat. J. Algebra Comput. 22(7) (2012), 1250075, 23.Google Scholar
Schützenberger, M. P., ‘Sur le produit de concaténation non ambigu’, Semigroup Forum 13(1) (1976/77), 47–75.Google Scholar
Seif, S. and Szabó, C., ‘Computational complexity of checking identities in 0-simple semigroups and matrix semigroups over finite fields’, Semigroup Forum 72(2) (2006), 207–222.Google Scholar
Steindl, M., ‘The subpower membership problem for bands’, J. Algebra 489(Supplement C) (2017), 529–551.Google Scholar
Willard, R., ‘Four unsolved problems in congruence permutable varieties’. Talk at International Conference on Order, Algebra, and Logics, Vanderbilt University, Nashville, June 12–16, 2007.Google Scholar