Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T09:02:23.923Z Has data issue: false hasContentIssue false
  • English
  • Français

On projective-symmetric spaces

Published online by Cambridge University Press:  09 April 2009

Bandana Gupta
Bandana Gupta
Affiliation:
Department of Pure MathematicsCalcutta University.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with a type of Remannian space Vn (n ≧ 2) for which the first covariant dervative of Weyl's projective curvature tensor 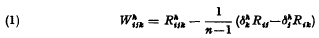is everywhere zero, that is where comma denotes covariant differentiation with respect to the metric tensor gij of Vn. Such a space has been called a projective-symmetric space by Gy. Soós [1]. We shall denote such an n-space by ψn. It will be proved in this paper that decomposable Projective-Symmetric spaces are symmetric in the sense of Cartan. In sections 3, 4 and 5 non-decomposable spaces of this kind will be considered in relation to other well-known classes of Riemannian spaces defined by curvature restrictions. In the last section the question of the existence of fields of concurrent directions in a ψ will be discussed.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 4 , Issue 1 , February 1964 , pp. 113 - 121
Copyright
Copyright © Australian Mathematical Society 1964

References

[1]Soós, Gy.Über die Geodätischen Abbildugen von Riemannschen Räumen auf Projectiv-Symmetrische Riemannsche Räume, Acta Math. Acad. Sci. Hung. 9 (1958).CrossRefGoogle Scholar
[2]Hlavatý, V., Rigid motion in a Riemannian space Vn. II. A regular Vn Rend. Circolo Matematico Palermo, (2) 9 (1960), 15–16.Google Scholar
[3]Ficken, F. A., The Riemannian and affine differential geometry of product spaces, Annals of Mathematics (2), 40 (1939). 892–913.CrossRefGoogle Scholar
[4]Schirokov, P., On the concurrent directions in Riemannian spaces, Bull. Physico-Math. Soc. Kazan. (3) 8 (1934–1935), 77–87 (Russian).Google Scholar