Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T09:19:58.208Z Has data issue: false hasContentIssue false
  • English
  • Français

ON POSITIVE PROPORTION OF RANK-ZERO TWISTS OF ELLIPTIC CURVES OVER 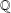$\mathbb{Q}$

Part of: Arithmetic algebraic geometry Curves

Published online by Cambridge University Press:  07 November 2014

MAOSHENG XIONG
MAOSHENG XIONG*
Affiliation:
Department of Mathematics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Extending the idea of Dabrowski [‘On the proportion of rank 0 twists of elliptic curves’, C. R. Acad. Sci. Paris, Ser. I 346 (2008), 483–486] and using the 2-descent method, we provide three general families of elliptic curves over 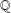$\mathbb{Q}$ such that a positive proportion of prime-twists of such elliptic curves have rank zero simultaneously.

Keywords

elliptic curves2-descentSelmer grouprank

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 14H52: Elliptic curves
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 2 , April 2015 , pp. 281 - 288
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Atake, D., ‘On elliptic curves with large Tate–Shafarevich groups’, J. Number Theory 87 (2001), 282–300.Google Scholar
Breuil, C., Conrad, B., Diamond, F. and Taylor, R., ‘On the modularity of ellipitc curves over ℚ’, J. Amer. Math. Soc. 14 (2001), 843–939.Google Scholar
Chen, J. R., ‘On the representation of a large even number as the sum of a prime and the product of at most two primes’, Sci. Sinica 16 (1973), 157–176.Google Scholar
Dabrowski, A., ‘On the proportion of rank 0 twists of elliptic curves’, C. R. Acad. Sci. Paris, Ser. I 346 (2008), 483–486.CrossRefGoogle Scholar
Dabrowski, A. and Wieczorek, M., ‘On the equation y 2 = x (x − 2m)(x + 1 − 2m)’, J. Number Theory 214 (2007), 364–379.Google Scholar
Feng, K. and Xiong, M., ‘On elliptic curves y 2 = x 3 − n 2x with rank zero’, J. Number Theory 109(1) (2004), 1–26.CrossRefGoogle Scholar
Feng, K. and Xiong, M., ‘On Selmer groups and Tate–Shafarevich groups for elliptic curves y 2 = x 3 − n 3’, Mathematika 58(2) (2012), 236–274.Google Scholar
Feng, K. and Xue, Y., ‘New series of odd non-congruent numbers’, Sci. China Ser. A 49(11) (2006), 1642–1654.Google Scholar
Goldfeld, D., ‘Conjectures on elliptic curves over quadratic fields’, in: Number Theory, Carbondale 1979, Lecture Notes in Mathematics, 751 (ed. Nathanson, M. B.) (Springer, Berlin, 1979), 108–118.Google Scholar
Hoffstein, J. and Luo, W. , ‘Nonvanishing of L-series and the combinatorial sieve’, Math. Res. Lett. 4 (1997), 435–444.CrossRefGoogle Scholar
Iwaniec, H., ‘Almost-primes represented by quadratic polynomials’, Invent. Math. 47 (1978), 171–188.Google Scholar
Iwaniec, H. and Sarnak, P., ‘The non-vanishing of central values of automorphic L-functions and Landau–Siegel zeros’, Israel J. Math. 120 (2000), 155–177.Google Scholar
James, K., ‘L-series with non-zero central critical value’, J. Amer. Math. Soc. 11 (1998), 635–641.Google Scholar
Kohnen, W., ‘On the proportion of quadratic twists of L-functions attached to cusp forms not vanishing at the central point’, J. reine angew. Math. 508 (1999), 179–187.CrossRefGoogle Scholar
Kolyvagin, V. A., ‘Finiteness of E (ℚ) and Ш (E, ℚ) for a subclass of Weil curves’, Izv. Acad. Nauk USSR 52 (1988), 522–540 (in Russian).Google Scholar
Ono, K. and Skinner, C., ‘Non-vanishing of quadratic twists of modular L-functions’, Invent. Math. 34 (1998), 651–660.Google Scholar
Silverman, J. H., The Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, 106 (Springer, New York, 1986).Google Scholar
Vatsal, V., ‘Rank-one twists of a certain elliptic curve’, Math. Ann. 311 (1998), 791–794.CrossRefGoogle Scholar
Waldspurger, J. L., ‘Sur les coefficients de Fourier des formes modulaires de poids demi-entier’, J. Math. Pures Appl. (9) 60 (1981), 375–484.Google Scholar
Yu, G., ‘On the quadratic twists of a family of elliptic curves’, Mathematika 52(1–2) (2005), 139–154.CrossRefGoogle Scholar