Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-20T18:38:19.652Z Has data issue: false hasContentIssue false
  • English
  • Français

ON 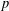$p$-GROUPS WITH AUTOMORPHISM GROUPS RELATED TO THE CHEVALLEY GROUP 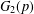$G_{2}(p)$

Part of: Representation theory of groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  08 January 2020

JOHN BAMBERG Open the ORCID record for JOHN BAMBERG [Opens in a new window] ,
SAUL D. FREEDMAN Open the ORCID record for SAUL D. FREEDMAN [Opens in a new window]  and
LUKE MORGAN
JOHN BAMBERG
Affiliation:
Centre for the Mathematics of Symmetry and Computation, The University of Western Australia, 35 Stirling Highway, Crawley, WA6009, Australia email [email protected]
SAUL D. FREEDMAN*
Affiliation:
Centre for the Mathematics of Symmetry and Computation, The University of Western Australia, 35 Stirling Highway, Crawley, WA6009, Australia email [email protected]
LUKE MORGAN
Affiliation:
Centre for the Mathematics of Symmetry and Computation, The University of Western Australia, 35 Stirling Highway, Crawley, WA6009, Australia email [email protected]
*
✉ email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 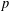$p$ be an odd prime. We construct a 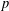$p$-group 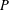$P$ of nilpotency class two, rank seven and exponent 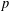$p$, such that 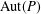$\text{Aut}(P)$ induces 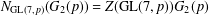$N_{\text{GL}(7,p)}(G_{2}(p))=Z(\text{GL}(7,p))G_{2}(p)$ on the Frattini quotient 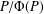$P/\unicode[STIX]{x1D6F7}(P)$. The constructed group 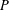$P$ is the smallest 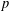$p$-group with these properties, having order 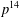$p^{14}$, and when 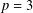$p=3$ our construction gives two nonisomorphic $p$-groups. To show that $P$ satisfies the specified properties, we study the action of 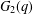$G_{2}(q)$ on the octonion algebra over 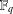$\mathbb{F}_{q}$, for each power 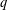$q$ of 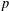$p$, and explore the reducibility of the exterior square of each irreducible seven-dimensional 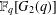$\mathbb{F}_{q}[G_{2}(q)]$-module.

Keywords

p-groupexterior squareG2(q)

MSC classification

Primary: 20C33: Representations of finite groups of Lie type
Secondary: 20G15: Linear algebraic groups over arbitrary fields 20D15: Nilpotent groups, $p$-groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 3 , June 2020 , pp. 321 - 331
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author acknowledges the support of the Australian Research Council Future Fellowship FT120100036. The second author was supported by a Hackett Foundation Alumni Honours Scholarship, a Hackett Postgraduate Research Scholarship, and an Australian Government Research Training Program Scholarship at The University of Western Australia. The third author was supported by the Australian Research Council grant DE160100081.

†

Current address: School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK.

‡

Current address: UP FAMNIT, University of Primorska, Glagoljaška 8, 6000 Koper, Slovenia. Also affiliated with: UP IAM, University of Primorska, Muzejski trg 2, 6000 Koper, Slovenia.

References

Aschbacher, M., ‘On the maximal subgroups of the finite classical groups’, Invent. Math. 76(3) (1984), 469–514.CrossRefGoogle Scholar
Bamberg, J., Glasby, S. P., Morgan, L. and Niemeyer, A. C., ‘Maximal linear groups induced on the Frattini quotient of a p-group’, J. Pure Appl. Algebra 222(10) (2018), 2931–2951.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265.CrossRefGoogle Scholar
Bray, J. N., Holt, D. F. and Roney-Dougal, C. M., The Maximal Subgroups of the Low-Dimensional Finite Classical Groups, London Mathematical Society Lecture Note Series, 407 (Cambridge University Press, Cambridge, 2013).CrossRefGoogle Scholar
Bryant, R. M. and Kovács, L. G., ‘Lie representations and groups of prime power order’, J. Lond. Math. Soc. (2) 17(3) (1978), 415–421.CrossRefGoogle Scholar
Eick, B., Leedham-Green, C. R. and O’Brien, E. A., ‘Constructing automorphism groups of p-groups’, Comm. Algebra 30(5) (2002), 2271–2295.CrossRefGoogle Scholar
Gow, R., ‘Subspaces of $7\times 7$ skew-symmetric matrices related to the group $G_{2}$’, Preprint, 2008, arXiv:0811.1298.Google Scholar
Holt, D. F., Eick, B. and O’Brien, E. A., Handbook of Computational Group Theory, Discrete Mathematics and its Applications (Boca Raton) (Chapman & Hall/CRC, Boca Raton, FL, 2005).CrossRefGoogle Scholar
Humphreys, J. E., Modular Representations of Finite Groups of Lie Type, London Mathematical Society Lecture Note Series, 326 (Cambridge University Press, Cambridge, 2006).Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (AMS Chelsea Publishing, Providence, RI, 2006).Google Scholar
Jacobson, N., Exceptional Lie Algebras, Lecture Notes in Pure and Applied Mathematics, 1 (Marcel Dekker, New York, 1971).Google Scholar
Kleidman, P. and Liebeck, M., The Subgroup Structure of the Finite Classical Groups, London Mathematical Society Lecture Note Series, 129 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Liebeck, M. W., ‘On the orders of maximal subgroups of the finite classical groups’, Proc. Lond. Math. Soc. (3) 50(3) (1985), 426–446.CrossRefGoogle Scholar
Lübeck, F., ‘Small degree representations of finite Chevalley groups in defining characteristic’, LMS J. Comput. Math. 4 (2001), 135–169.CrossRefGoogle Scholar
O’Brien, E. A., ‘The p-group generation algorithm’, J. Symbolic Comput. 9(5–6) (1990), 677–698.CrossRefGoogle Scholar
Schröder, A. K., ‘The maximal subgroups of the classical groups in dimension 13, 14 and 15’, PhD Thesis, School of Mathematics and Statistics, University of St Andrews, 2015.Google Scholar
Wilson, R. A., The Finite Simple Groups, Graduate Texts in Mathematics, 251 (Springer, London, 2009).CrossRefGoogle Scholar