Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T04:49:57.349Z Has data issue: false hasContentIssue false
  • English
  • Français

On odd perfect numbers (II), multiperfect numbers and quasiperfect numbers

Published online by Cambridge University Press:  09 April 2009

Graeme L. Cohen
Graeme L. Cohen
Affiliation:
School of Mathematical Sciences The New South Wales Institute of Technology P.O. Box 123 Broadway NSW 2007 Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

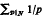Let N be a positive integer. This paper is concerned with obtaining bounds for (p prime), when N is an odd perfect number, a multiperfect number, or a quasiperfect number, under assumptions on the existence of such numbers (where none is known) and whether 3 and 5 are divisors. We argue that our new lower bounds in the case of odd perfect numbers are not likely to be significantly improved further. Triperfect numbers are investigated in some detail, and it is shown that an odd triperfect number must have at least nine distinct prime factors.

1980 Mathematics subject classification (Amer. Math. Soc.): 10 A 20.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 29 , Issue 3 , May 1980 , pp. 369 - 384
Copyright
Copyright © Australian Mathematical Society 1980

References

Abbott, H. L.Aull, Ezra Brown and D. Suryanarayana (1973), 'Quasiperfect numbers', Ada Arith. 22, 439–447; (1976), 'Corrections to the paper “Quasiperfect numbers”', Acta Arith. 29, 427–428.CrossRefGoogle Scholar
Cohen, G. L. (1978), 'On odd perfect numbers', Fibonacci Quart 16, 523–527.Google Scholar
Kishore, Masao (1978), 'Odd integers N with five distinct prime factors for which 2–10–12Math. Comp. 32, 303–309.Google Scholar
Krawczyk, Andrzej (1972), 'Uogo1nienie problemu Perisastriego', Prace Nauk. Inst. Mat. Fiz. Teoret. Politechn. Wroclaw. Ser. Studia i Materialy No. 6 Zagadnienia kombinatoryczne, 67–70 (English summary).Google Scholar
Suryanarayana, D. (1963), 'On odd perfect numbers II', Proc. Amer. Math. Soc. 14, 896–904.CrossRefGoogle Scholar
Suryanarayana, D. and Peter Hagis, Jr. (1970), 'A theorem concerning odd perfect numbers', Fibonacci Quart. 8, 337–346, 374.Google Scholar