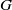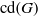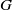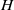Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yan, Yan Xiong
Xu, Hai Jing
and
Chen, Gui Yun
2015.
A characterization of almost simple K 3-groups.
Acta Mathematica Sinica, English Series,
Vol. 31,
Issue. 11,
p.
1739.
ALAVI, SEYED HASSAN
DANESHKHAH, ASHRAF
and
JAFARI, ALI
2016.
GROUPS WITH THE SAME CHARACTER DEGREES AS SPORADIC ALMOST SIMPLE GROUPS.
Bulletin of the Australian Mathematical Society,
Vol. 94,
Issue. 2,
p.
254.
Yan, Yanxiong
Zhang, Liangcai
Xu, Haijing
and
Chen, Guiyun
2016.
Recognizing the automorphism groups of Mathieu groups through their orders and large degrees of their irreducible characters.
Chinese Annals of Mathematics, Series B,
Vol. 37,
Issue. 4,
p.
495.
Sayanjali, Zohreh
Akhlaghi, Zeinab
and
Khosravi, Behrooz
2019.
Recognition of
$${\mathrm {PSL}}(2, p^{2})$$
PSL
(
2
,
p
2
)
by Order and Some Properties on Character Degrees.
Bulletin of the Iranian Mathematical Society,
Vol. 45,
Issue. 6,
p.
1777.
Qin, Chao
Yan, Yanxiong
Shum, Karping
and
Chen, Guiyun
2019.
Mathieu groups and its degree prime-power graphs.
Communications in Algebra,
Vol. 47,
Issue. 10,
p.
4173.
Moghadam, S. Madady
and
Iranmanesh, A.
2021.
Groups with the same character degrees as sporadic quasisimple groups.
Communications in Algebra,
Vol. 49,
Issue. 5,
p.
1966.
Liu, Xin
Chen, Guiyun
and
Yan, Yanxiong
2021.
A new characterization of the automorphism groups of Mathieu groups.
Open Mathematics,
Vol. 19,
Issue. 1,
p.
1245.
Alavi, Seyed Hassan
Daneshkhah, Ashraf
and
Zafarabad, Yazdan Momeni
2023.
Groups with the same character degrees as almost simple Suzuki groups.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 09,
Alavi, Seyed Hassan
2023.
On groups with the same character degrees as almost simple groups with socle small Ree groups.
Communications in Algebra,
Vol. 51,
Issue. 10,
p.
4372.