Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T08:14:44.707Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GRADED SYMMETRIC CELLULAR ALGEBRAS

Part of: Rings and algebras with additional structure Conditions on elements Representation theory of rings and algebras

Published online by Cambridge University Press:  29 July 2019

YANBO LI  and
DEKE ZHAO
YANBO LI*
Affiliation:
School of Mathematics and Statistics, Northeastern University at Qinhuangdao, Qinhuangdao066004, China email [email protected]
DEKE ZHAO
Affiliation:
School of Applied Mathematics, Beijing Normal University at Zhuhai, Zhuhai519087, China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $A=\bigoplus _{i\in \mathbb{Z}}A_{i}$ be a finite-dimensional graded symmetric cellular algebra with a homogeneous symmetrizing trace of degree 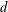$d$. We prove that if 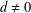$d\neq 0$ then 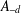$A_{-d}$ contains the Higman ideal 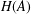$H(A)$ and 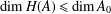$\dim H(A)\leq \dim A_{0}$, and provide a semisimplicity criterion for 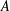$A$ in terms of the centralizer of 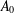$A_{0}$.

Keywords

(graded) cellular algebrasymmetric algebraHigman idealcentralizer

MSC classification

Primary: 16W50: Graded rings and modules
Secondary: 16G30: Representations of orders, lattices, algebras over commutative rings 16U70: Center, normalizer (invariant elements)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 3 , June 2020 , pp. 349 - 362
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Li is supported by the Natural Science Foundation of Hebei Province, China (A2017501003) and the Science and Technology support program of Northeastern University at Qinhuangdao (No. XNK201601). Zhao is supported partly by NSFC 11571341, 11671234, 11871107.

References

Andersen, H. H., Stroppel, C. and Tubbenhauer, D., ‘Cellular structures using U q-tilting modules’, Pacific J. Math. 292 (2018), 21–59.Google Scholar
Auslander, M., Reiten, I. and Smalo, S. O., Representation Theory of Artin Algebras (Cambridge University Press, Cambridge, 1995).Google Scholar
Beilinson, A., Ginzburg, V. and Soergel, W., ‘Koszul duality patterns in representation theory’, J. Amer. Math. Soc. 9 (1996), 473–528.Google Scholar
Brundan, J. and Kleshchev, A., ‘Blocks of cyclotomic Hecke algebras and Khovanov–Lauda algebras’, Invent. Math. 178 (2009), 451–484.Google Scholar
Brundan, J. and Kleshchev, A., ‘Graded deconposition numbers for cyclotomic Hecke algebras’, Adv. Math. 222 (2009), 1883–1942.Google Scholar
Brundan, J., Kleshchev, A. and Wang, W., ‘Graded Specht modules’, J. reine angew. Math. 655 (2011), 61–87.Google Scholar
Brundan, J. and Stroppel, C., ‘Highest weight categories arising from Khovanov’s diagram algebra I: Cellularity’, Mosc. Math. J. 11 (2011), 685–722.Google Scholar
Brundan, J. and Stroppel, C., ‘Highest weight categories arising from Khovanov’s diagram algebra III: Category 𝓞’, Represent. Theory 15 (2011), 170–243.Google Scholar
Brundan, J. and Stroppel, C., ‘Gradings on walled Brauer algebras and Khovanov’s arc algebra’, Adv. Math. 231 (2012), 709–773.Google Scholar
Cline, E., Parshall, B. and Scott, L., Algebraic Groups and Lie Groups: A Volume of Papers in Honour of the Late R.W. Richardson, Australian Mathematical Lecture Series, 9 (ed. Lehrer, G. I.) (Cambridge University Press, Cambridge, 1997), 105–125.Google Scholar
Fuller, K. R. and Zimmermann-Huisgen, B., ‘On the generalized Nakayama conjecture and the Cartan determinant problem’, Trans. Amer. Math. Soc. 294 (1986), 679–691.Google Scholar
Geck, M., ‘Hecke algebras of finite type are cellular’, Invent. Math. 169 (2007), 501–517.Google Scholar
Graham, J. J., ‘Modular representations of Hecke algebras and related algebras’, PhD thesis, Sydney University, 1995.Google Scholar
Graham, J. J. and Lehrer, G. I., ‘Cellular algebras’, Invent. Math. 123 (1996), 1–34.Google Scholar
Hu, J. and Mathas, A., ‘Graded cellular bases for the cyclotomic Khovanov–Lauda–Rouquier algebras of type A’, Adv. Math. 225 (2010), 598–642.Google Scholar
Hu, J. and Mathas, A., ‘Cyclotomic quiver Schur algebras for linear quivers’, Proc. Lond. Math. Soc. (3) 110 (2015), 1315–1386.Google Scholar
Hu, J. and Mathas, A., ‘Seminormal forms and cyclotomic quiver Hecke algebras of type A’, Math. Ann. 364 (2016), 1189–1254.Google Scholar
Kazhdan, D. and Lusztig, G., ‘Representations of Coxeter groups and Hecke algebras’, Invent. Math. 53 (1979), 165–184.Google Scholar
Li, Y. B., ‘Centres of symmetric cellular algebras’, Bull. Aust. Math. Soc. 82 (2010), 511–522.Google Scholar
Li, Y. B., ‘Nakayama automorphisms of Frobenius cellular algebras’, Bull. Aust. Math. Soc. 86 (2012), 515–524.Google Scholar
Li, Y. B., ‘Radicals of symmetric cellular algebras’, Colloq. Math. 133 (2013), 67–83.Google Scholar
Li, Y. B., ‘On the radical of the group algebra of a symmetric group’, J. Algebra Appl. 16(9) (2017), 1750175.Google Scholar
Li, Y. B. and Xiao, Z. K., ‘On cell modules of symmetric cellular algebras’, Monatsh. Math. 168 (2012), 49–64.Google Scholar
Li, Y. B. and Zhao, D. K., ‘Projective cell modules of Frobenius cellular algebras’, Monatsh. Math. 175 (2014), 283–291.Google Scholar
Liu, Y. M., Zhou, G. D. and Zimmermann, A., ‘Higman ideal, stable Hochschild homology and Auslander–Reiten conjecture’, Math. Z. 270 (2012), 759–781.Google Scholar
Plaza, D. and Ryom-Hansen, S., ‘Graded cellular bases for Temperley-Lieb algebras of type A and B’, J. Algebraic Combin. 40 (2014), 137–177.Google Scholar
Rouquier, R., ‘Derived equivalences and finite dimensional algebras’, in: Proc. Int. Congr. Math., Madrid, 2006, II (EMS Publishing House, Zurich, 2006), 191–221.Google Scholar
Xi, C. C., ‘Partition algebras are cellular’, Compos. Math. 119 (1999), 99–109.Google Scholar
Xi, C. C., ‘On the quasi-heredity of Birman–Wenzl algebras’, Adv. Math. 154 (2000), 280–298.Google Scholar