Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T09:25:01.490Z Has data issue: false hasContentIssue false
  • English
  • Français

On distributions whose moments are majorated by the moments of a known distribution*

Published online by Cambridge University Press:  09 April 2009

R. G. Laha  and
Eugene Lukacs
R. G. Laha
Affiliation:
The Catholic University of America.
Eugene Lukacs
Affiliation:
The Catholic University of America.
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F(x) be a distribution function and denote by 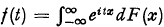its characteristic function and by 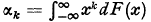its moment of order k H. Milicer-Grużewska [2]has derived the following theorem: Suppose that F(x) has moments of all orders and that they satisfy the relations. where while C is a positive constant. Then f(t) is an entire function of order not exceeding two. The proof given by H. Milicer-Gruzewska is rather complicated, moreover the restriction (1.2) seems to be artificial and motivated only by the particular method of proof. We note that condition (1.1) means that the moments of F (x) are majorated by the moments of a normal distribution and we use this remark to generalize the problem.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 1 , Issue 1 , August 1959 , pp. 113 - 115
Copyright
Copyright © Australian Mathematical Society 1959

References

[1]Boas, R. P., Sur les séries et intégrales de Fourier à coefficients positifs. C.R. Acad. Sci. Paris, vol. 228 (1949), 1837–1838.Google Scholar
[2]Milicer-Grużewska, H., On the law of probability and the characteristic function of the standardized sum of equivalent variables. Soc. Sci. Lett. Varsovie, C.R. Cl. III, Sci. Math. Phys. 42 (1949), (1952), 99–143.Google Scholar