Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T21:08:54.103Z Has data issue: false hasContentIssue false
  • English
  • Français

On digital distribution in some integer sequences

Published online by Cambridge University Press:  09 April 2009

B. D. Craven
B. D. Craven
Affiliation:
University of Melbourne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Although the harmonic series 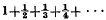diverges, there is a sense in which it “nearly converges”. Let N denote the set of all positive integers, and S a subset of N. Then there are various sequences S for which 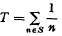converges, but for which the “omitted sequence” N–S is, in intuitive sense, sparse, compared with N. For example, Apostol [1] (page 384) quotes, without proof the case where S is the set of all Positive integers whose decimal representation does not invlove the digit zero (e.g. 7∈S but 101 ∉ S); then (1) converges, with T < 90.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 5 , Issue 3 , August 1965 , pp. 325 - 330
Copyright
Copyright © Australian Mathematical Society 1965

References

[1]Apostol, T. M., Mathematical Analysis. (Addison-Wesley, 1957).Google Scholar
[2]Landau, E., Handbuch der Lehre von der Verteilung der Primzahlen, Vol. I.Google Scholar
[3]LeVeque, W. J., Topics in Number Theory, Vol. II. (Addison-Wesley, 1956).Google Scholar