Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T08:05:00.748Z Has data issue: false hasContentIssue false
  • English
  • Français

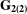ON COMPACT HOMOGENEOUS $\mathbf{\text{G}_{2(2)}}$-MANIFOLDS

Part of: Global differential geometry

Published online by Cambridge University Press:  04 September 2019

WOLFGANG GLOBKE Open the ORCID record for WOLFGANG GLOBKE [Opens in a new window]
WOLFGANG GLOBKE*
Affiliation:
Faculty of Mathematics, Oskar-Morgenstern-Platz 1, Universität Wien, 1090Vienna, Austria
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that among all compact homogeneous spaces for an effective transitive action of a Lie group whose Levi subgroup has no compact simple factors, the seven-dimensional flat torus is the only one that admits an invariant torsion-free 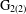$\text{G}_{2(2)}$-structure.

Keywords

G2(2) holonomycompact homogeneous spacespseudo-Riemannian manifolds

MSC classification

Primary: 53C50: Lorentz manifolds, manifolds with indefinite metrics
Secondary: 53C30: Homogeneous manifolds 53C29: Issues of holonomy
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 1 , February 2021 , pp. 71 - 80
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by M. Murray

Wolfgang Globke is supported by the Austrian Science Fund FWF grant I 3248.

References

Baues, O., Globke, W. and Zeghib, A., ‘Isometry Lie algebras of indefinite homogeneous spaces of finite volume’, Proc. Lond. Math. Soc. 119(4) (2019), 1115–1148.Google Scholar
Besse, A. L., Einstein Manifolds, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 10 (Springer, Berlin, 1987).CrossRefGoogle Scholar
Bonan, E., ‘Sur les variétés Riemanniennes à groupe d’holonomie G2 ou Spin(7)’, C. R. Math. Acad. Sci. Paris 262 (1966), 127–129.Google Scholar
Fino, A. and Luján, I., ‘Torsion-free G2(2) ∗ -structures with full holonomy on nilmanifolds’, Adv. Geom. 15(3) (2015), 381–392.CrossRefGoogle Scholar
Globke, W. and Nikolayevsky, Y., ‘Compact pseudo-Riemannian homogeneous Einstein manifolds in low dimension’, Differential Geom. Appl. 54(Part B) (2017), 475–489.Google Scholar
Kath, I., ‘Nilpotent metric Lie algebras of small dimension’, J. Lie Theory 17 (2007), 41–61.Google Scholar
Kath, I., ‘Indefinite symmetric spaces with G2(2) -structure’, J. Lond. Math. Soc. 87(2) (2013), 853–876.CrossRefGoogle Scholar
Lê, H. V. and Munir, M., ‘Classification of compact homogeneous spaces with invariant G2 -structures’, Adv. Geom. 12(2) (2012), 303–328.CrossRefGoogle Scholar
Leistner, T., Nurowski, P. and Sagerschnig, K., ‘New relations between G2 -geometries in dimensions 5 and 7’, Int. J. Math. 28(13) (2017), 1750094.Google Scholar