Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Quine, M. P.
and
Seneta, E.
1969.
A LIMIT THEOREM FOR THE GALTON‐WATSON PROCESS WITH IMMIGRATION.
Australian Journal of Statistics,
Vol. 11,
Issue. 3,
p.
166.
Seneta, E.
1969.
Functional equations and the Galton-Watson process.
Advances in Applied Probability,
Vol. 1,
Issue. 1,
p.
1.
Seneta, E.
1969.
Functional equations and the Galton-Watson process.
Advances in Applied Probability,
Vol. 1,
Issue. 1,
p.
1.
Pollak, Edward
1971.
On survival probabilities and extinction times for some branching processes.
Journal of Applied Probability,
Vol. 8,
Issue. 4,
p.
633.
Pakes, A. G.
1971.
A branching process with a state dependent immigration component.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
301.
Fahady, K. S.
Quine, M. P.
and
Vere-Jones, D.
1971.
Heavy traffic approximations for the Galton-Watson process.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
282.
Fahady, K. S.
Quine, M. P.
and
Vere-Jones, D.
1971.
Heavy traffic approximations for the Galton-Watson process.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
282.
Pakes, A. G.
1971.
On a Theorem of Quine and Seneta for the Galton‐Watson Process With Immigration.
Australian Journal of Statistics,
Vol. 13,
Issue. 3,
p.
159.
Pakes, A. G.
1971.
A branching process with a state dependent immigration component.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
301.
Pakes, A.G.
1971.
Some results for the supercritical branching process with immigration.
Mathematical Biosciences,
Vol. 11,
Issue. 3-4,
p.
355.
Pollak, Edward
1971.
On survival probabilities and extinction times for some branching processes.
Journal of Applied Probability,
Vol. 8,
Issue. 04,
p.
633.
Pakes, A.G.
1972.
Limit theorems for an age-dependent branching process with immigration.
Mathematical Biosciences,
Vol. 14,
Issue. 3-4,
p.
221.
Pakes, A. G.
1972.
Further results on the critical Galton-Watson process with immigration.
Journal of the Australian Mathematical Society,
Vol. 13,
Issue. 3,
p.
277.
Ney, Peter
1974.
Critical branching processes.
Advances in Applied Probability,
Vol. 6,
Issue. 3,
p.
434.
Pollak, Edward
1974.
Survival probabilities and extinction times for some multitype branching processes.
Advances in Applied Probability,
Vol. 6,
Issue. 3,
p.
446.
Ney, Peter
1974.
Critical branching processes.
Advances in Applied Probability,
Vol. 6,
Issue. 3,
p.
434.
Pollak, Edward
1974.
Survival probabilities and extinction times for some multitype branching processes.
Advances in Applied Probability,
Vol. 6,
Issue. 3,
p.
446.
Agresti, Alan
1974.
Bounds on the extinction time distribution of a branching process.
Advances in Applied Probability,
Vol. 6,
Issue. 2,
p.
322.
Agresti, Alan
1974.
Bounds on the extinction time distribution of a branching process.
Advances in Applied Probability,
Vol. 6,
Issue. 2,
p.
322.
Hwang, Tea-Yuan
and
Wang, Nae-Sheng
1979.
On best fractional linear generating function bounds.
Journal of Applied Probability,
Vol. 16,
Issue. 2,
p.
449.


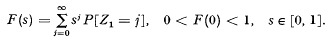
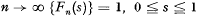 (Harris [1], Chapter 1). In particular, extinction is certain.
(Harris [1], Chapter 1). In particular, extinction is certain.