Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T08:34:36.240Z Has data issue: false hasContentIssue false
  • English
  • Français

On a result of Cassels

Published online by Cambridge University Press:  09 April 2009

R. T. Worley
R. T. Worley
Affiliation:
Monash University Clayton, Vic. 3168
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let α be an irrational algebraic number of degree k over the rationals. Let K denote the field generated by α over the rationals and let a denote the ideal denominator of α. Then Cassels [3] has shown that for sufficiently large integral N > 0 distinctly more than half the integers n,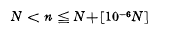 are such that (n+α)a is divisible by a prime ideal pn which does not divide (m+α)a for any integer m ≠ n satisfying 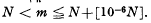. The purpose of this note is to point out that minor modification of Cassel's proof enables the extension of the interval for n from 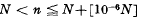to 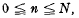, and to derive results on the proportion of values n, for which the values f(n) of a given integral polynomial in n are divisible by a prime p > N.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 2 , May 1970 , pp. 191 - 194
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]de Bruijn, N. G., ‘On the number of positive integers ≦ x and free of prime divisors > y’, Proc. K. Nederl. Akad. Wetensch. 54 (1951) 50–60.CrossRefGoogle Scholar
[2]Buchstab, A. A., ‘On those numbers in an arithmetic progression all prime factors of which are small in magnitude’, Doklady Akad. Nauk SSSR 67 (1949) 5–8.Google Scholar
[3]Cassels, J. W. S., ‘Footnote to a note of Davenport and Heilbronn’, J. Lond. Math. Soc. 36 (1961) 177–184.CrossRefGoogle Scholar
[4]Chowla, S. and Vijayaraghavan, T., ‘On the largest prime divisors of numbers’, J. Ind. Math. Soc. (N.S.) 11 (1947) 31–37.Google Scholar
[5]Ramaswami, V., 'The number of positive integers < x and free of prime divisors > xe, and a problem of S. Pillai, Duke Math. J. 16 (1949) 99–109.CrossRefGoogle Scholar