Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T07:26:35.041Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A PROBLEM POSED BY MAHLER

Part of: Diophantine approximation, transcendental number theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  11 November 2015

DIEGO MARQUES  and
JOHANNES SCHLEISCHITZ
DIEGO MARQUES
Affiliation:
Department of Mathematics, University of Brasilia, Brasilia, Df, Brazil email [email protected]
JOHANNES SCHLEISCHITZ*
Affiliation:
Institute of Mathematics, University of Natural Resources and Life Sciences, Vienna, Augasse 2–6, 1090 Vienna, Austria email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Maillet proved that the set of Liouville numbers is preserved under rational functions with rational coefficients. Based on this result, a problem posed by Mahler is to investigate whether there exist entire transcendental functions with this property or not. For large parametrized classes of Liouville numbers, we construct such functions and moreover we show that they can be constructed such that all their derivatives share this property. We use a completely different approach than in a recent paper, where functions with a different invariant subclass of Liouville numbers were constructed (though with no information on derivatives). More generally, we study the image of Liouville numbers under analytic functions, with particular attention to 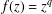$f(z)=z^{q}$, where 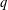$q$ is a rational number.

Keywords

Liouville numberstranscendental functionexceptional setcontinued fractions

MSC classification

Primary: 11J04: Homogeneous approximation to one number
Secondary: 11J82: Measures of irrationality and of transcendence 11K60: Diophantine approximation
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 1 , February 2016 , pp. 86 - 107
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Alniacik, K., ‘On Mahler’s U-numbers’, Amer. J. Math. 105(6) (1983), 1347–1356.CrossRefGoogle Scholar
Alniacik, K. and Saias, E., ‘Une remarque sur les G 𝛿 -denses’, Arch. Math. (Basel) 62 (1994), 425–426.CrossRefGoogle Scholar
Bugeaud, Y., Approximation by Algebraic Numbers, Cambridge Tracts in Mathematics, 160 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Bugeaud, Y., ‘On simultaneous rational approximation to a real number and its integral powers’, Ann. Inst. Fourier (Grenoble) 60(6) (2010), 2165–2182.CrossRefGoogle Scholar
Burger, E., ‘On Liouville decompositions in local fields’, Proc. Amer. Math. Soc. 124 (1996), 3305–3310.CrossRefGoogle Scholar
Burger, E. and Tubbs, R., Making Transcendence Transparent. An Intuitive Approach to Classical Transcendental Number Theory (Springer, New York, 2004), Ch. 6, 147–181.CrossRefGoogle Scholar
Chaves, A. P. and Marques, D., ‘An explicit family of U m -numbers’, Elem. Math. 69 (2014), 18–22.CrossRefGoogle Scholar
Conway, J. B., Functions of One Complex Variable I, 2nd edn (Springer, New York, 1978).CrossRefGoogle Scholar
Dirichlet, P. G. L., ‘Beweis des Satzes, dass jede unbegrenzte arithmetische Progression, deren erstes Glied und Differenz ganze Zahlen ohne gemeinschaftlichen Factor sind, unendlich viele Primzahlen enthält’, Abh. Akad. Wiss. Berlin 48 (1837), 45–81.Google Scholar
Erdős, P., ‘Representations of real numbers as sums and products of Liouville numbers’, Michigan Math. J. 9 (1962), 59–60.CrossRefGoogle Scholar
Gramain, F., ‘Functions entières arithmétiques: un Aperçu historique’, Publications IRMA université de Lille 6(1) (1984), 1–21.Google Scholar
Huang, J., Marques, D. and Mereb, M., ‘Algebraic values of transcendental functions at algebraic points’, Bull. Aust. Math. Soc. 82 (2010), 322–327.CrossRefGoogle Scholar
Jarnik, V., ‘Über die simultanen Diophantischen Approximationen’, Math. Z. 33 (1931), 505–543.CrossRefGoogle Scholar
Kumar, K., Thangadurai, R. and Waldschmidt, M., ‘Liouville numbers and Schanuel’s conjecture’, Arch. Math. 102 (2014), 59–70.CrossRefGoogle Scholar
LeVeque, W. J., ‘On Mahler’s U-numbers’, J. Lond. Math. Soc. (2) 28 (1953), 220–229.CrossRefGoogle Scholar
LeVeque, W. J., Topics in Number Theory, Vols. I and II (Dover, New York, 2002).Google Scholar
Mahler, K., ‘Some suggestions for further research’, Bull. Aust. Math. Soc. 21 (1984), 101–108.CrossRefGoogle Scholar
Maillet, E., Introduction a la theorie des nombres transcendants et des proprietes arithmetiques des fonctions (Gauthier-Villars, Paris, 1906).Google Scholar
Marques, D., ‘On the arithmetic nature of hypertranscendental functions at complex points’, Expo. Math. 29 (2011), 361–370.CrossRefGoogle Scholar
Marques, D. and Moreira, C. G., ‘On a variant of a question posed by K. Mahler concerning Liouville numbers’, Bull. Math. Aust. Soc. 91(1) (2015), 29–33.CrossRefGoogle Scholar
Marques, D. and Ramirez, J., ‘On transcendental analytic functions mapping an uncountable class of U-numbers into Liouville numbers’, Proc. Japan Acad. Sci. 91(2) (2015), 25–28.Google Scholar
Minkowski, H., Geometrie der Zahlen (Teubner, Leipzig, 2010).Google Scholar
Perron, O., Lehre von den Kettenbrüchen (Teubner, Stuttgart, 1913).Google Scholar
van der Poorten, A. J., ‘Transcendental entire functions mapping every algebraic number field into itself’, J. Aust. Math. Soc. 8 (1968), 192–193.CrossRefGoogle Scholar
Rieger, G. J., ‘Über die Lösbarkeit von Gleichungssystemen durch Liouville-Zahlen’, Arch. Math. 26(1) (1975), 40–43.CrossRefGoogle Scholar
Schleischitz, J., ‘On the spectrum of Diophantine approximation constants’, Mathematika, to appear.Google Scholar
Schmidt, W. M., ‘T-numbers do exist’, in: Symposia Mathematica, Vol. IV (INDAM, Rome, 1968/1969) (Academic Press, London, 1970), 3–26.Google Scholar
Schmidt, W. M. and Summerer, L., ‘Parametric geometry of numbers and applications’, Acta Arith. 140(1) (2009), 67–91.CrossRefGoogle Scholar
Schneider, T., Einführung in die transzendenten Zahlen (Springer, Berlin, 1957).CrossRefGoogle Scholar
Schwarz, W., ‘Liouville-Zahlen und der Satz von Baire’, Math.-Phys. Semesterber. 24 (1977), 84–87.Google Scholar
Silva, E., ‘Some results related to Liouville numbers’, Master’s Thesis, Universidade de Brasilia, 2015.Google Scholar
Sprindẑuk, V. G., ‘A proof of Mahler’s conjecture on the measure of the set of S-numbers’, Izv. Akad. Nauk SSSR Ser. Mat. 29 (1965), 379–436; English translation: Amer. Math. Soc. Transl. 51 (1966) 215–272.Google Scholar
Stäckel, P., ‘Ueber arithmetische Eingenschaften analytischer Functionen’, Math. Ann. 46(4) (1895), 513–520.CrossRefGoogle Scholar
Waldschmidt, M., ‘Recent advances in Diophantine approximation’, in: Number Theory, Analysis and Geometry (Springer, New York, 2012), 659–704.CrossRefGoogle Scholar