Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-27T15:45:44.649Z Has data issue: false hasContentIssue false
  • English
  • Français

Objets compacts dans les topos

Part of: Special categories

Published online by Cambridge University Press:  09 April 2009

Eduardo J. Dubuc  and
Jacques Penon
Eduardo J. Dubuc
Affiliation:
Departamento de Matematicas, Universidad de Buenos Aires, 1428 Buenos Aires, Argentina
Jacques Penon
Affiliation:
U.E.R. de Mathmatiques, Universit de Paris VII, Tours 4555, 2 Place Jussieu, 75005 Paris, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that compact topological spaces are those space K for which given any point x0 in any topological space X, and a neighborhood H of the fibre -1 {x0} KXX, then there exists a neighborhood U of x0 such that -1UH. If now 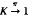is an object in an arbitrary topos, in the internal logic of the topos this property means that, for any A in and B in K, we have (-1AB)=AB. We introduce this formula as a definition of compactness for objects in an arbitrary topos. Then we prove that in the gross topoi of algebraic, analytic, and differential geometry, this property characterizes exactly the complete varieties, the compact (analytic) spaces, and the compact manifolds, respectively.

MSC classification

Secondary: 18B25: Topoi
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 40 , Issue 2 , April 1986 , pp. 203 - 217
Copyright
Copyright Australian Mathematical Society 1986

References

1Dubuc, E. J., Sur les modeles de la gomtrie diffrentielle synthtique, Cahiers Topologie Gom. Diffrentielle Vol. XX3, (1979).Google Scholar
2Dubuc, E. J., Open covers and infinitary operations in C-rings, Cahiers Topologie Gom. Diffrentielle, Vol. XXII3, (1981).Google Scholar
3Dubuc, E. J., C-schemes, Amer. J. Math. 103 (1981), 683690.CrossRefGoogle Scholar
4Hakim, M., Topos annals et schmas relatif, Ergeb. Math. Grenzgeb., Band 64 (Springer-Verlag, Berlin, Heidelberg, New York, 1972).Google Scholar
5Kock, A., Universal projective geometry; via topos theory, J. Pure Appl. Algebra 9 (1976), 124.Google Scholar
6Kock, A., Synthetic differential geometry (Cambridge University Press, Cambridge, England, 1981).Google Scholar
7Malgrange, B., Analytic spaces (Monographie N 17 de l'Enseignement Mathmatique, Genve 1968).Google Scholar
8Penon, J., Topologie et intuitionnisme, dans Journes Faisceaux et Logique, Mai 1981 (Universit Paris-Nord, Pr-publications Mathmatique (1982)).Google Scholar
9Penon, J., Manuscrits non-publis, a paraitre dans la these de doctorat, Paris VII.Google Scholar
10Spivak, M., A comprehensive introduction to differential geometry, Vol. 1, Publish or Perish (Brandeis University, 1970).Google Scholar