No CrossRef data available.
Article contents
Numerical Range of the Derivation of an Induced Operator
Published online by Cambridge University Press: 09 April 2009
Abstract
Let V be an n–dimensional inner product space over 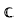 , let H be a subgroup of the symmetric group on {l,…, m}, and let x: H →
, let H be a subgroup of the symmetric group on {l,…, m}, and let x: H → 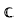 be an irreducible character. Denote by
be an irreducible character. Denote by 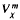 (H) the symmetry class of tensors over V associated with H and x. Let K (T) ∈ End(
(H) the symmetry class of tensors over V associated with H and x. Let K (T) ∈ End(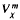 (H)) be the operator induced by T ∈ End(V), and let DK(T) be the derivation operator of T. The decomposable numerical range W*(DK(T)) of DK(T) is a subset of the classical numerical range W(DK(T)) of DK(T). It is shown that there is a closed star-shaped subset
(H)) be the operator induced by T ∈ End(V), and let DK(T) be the derivation operator of T. The decomposable numerical range W*(DK(T)) of DK(T) is a subset of the classical numerical range W(DK(T)) of DK(T). It is shown that there is a closed star-shaped subset 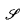 of complex numbers such that
of complex numbers such that
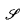 ⊆ W*(DK(T)) ⊆ W(DK(T)) = con
⊆ W*(DK(T)) ⊆ W(DK(T)) = con 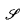
where conv 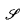 denotes the convex hull of
denotes the convex hull of 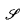 . In many cases, the set
. In many cases, the set 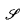 is convex, and thus the set inclusions are actually equalities. Some consequences of the results and related topics are discussed.
is convex, and thus the set inclusions are actually equalities. Some consequences of the results and related topics are discussed.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2007


