Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Porcu, E.
Gregori, P.
and
Mateu, J.
2007.
La descente et la montée étendues: the spatially d-anisotropic and the spatio-temporal case.
Stochastic Environmental Research and Risk Assessment,
Vol. 21,
Issue. 6,
p.
683.


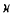 and use their properties to give a proof of the Lévy-Khinchin formula for an infinitely divisible probability distribution on
and use their properties to give a proof of the Lévy-Khinchin formula for an infinitely divisible probability distribution on 