Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T08:29:31.696Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the finite Fourier transform

Published online by Cambridge University Press:  09 April 2009

James L. Griffith
James L. Griffith
Affiliation:
University of New South Wales, Sydney, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. One of the best known theorems on the finite Fourier transform is:—The integral function F(z) is of the exponential type C and belongs to L2 on the real axis, if and only if, there exists an f(x) belonging to L2 (—C, C) such that (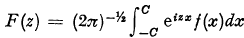 Additionally, if f(x) vanishes almost everywhere in a neighbourhood of C and also in a neighbourhood of —C, then F(z) is of an exponential type lower than C.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 1 , Issue 1 , August 1959 , pp. 95 - 98
Copyright
Copyright © Australian Mathematical Society 1959

References

[1]Boas, R. P. Jnr, Entire Functions, Academic Press, New York (1954).Google Scholar
[2]Doetsch, G., Handbuch der Laplace-Transformation, Bd 1, Birkhäuser, Basel (1950).CrossRefGoogle Scholar