Hostname: page-component-5cf477f64f-r2nwp Total loading time: 0 Render date: 2025-04-06T23:28:52.665Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on free products with a normal amalgamation

Published online by Cambridge University Press:  09 April 2009

R. A. Bryce
R. A. Bryce
Affiliation:
Department of MathematicsInstitute of Advanced Studies Australian National University Canberra, A.C.T.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is a consequence of the Kurosh subgroup theorem for free products that if a group has two decompositions 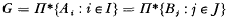where each Ai and each Bj is indecomposable, then I and J can be placed in one-to-one correspondence so that corresponding groups if not conjugate are infinite cycles. We prove here a corresponding result for free products with a normal amalgamation.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 3 , August 1968 , pp. 631 - 637
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Kurosh, A. G., The theory of groups, vol. II (Chelsea, New York, 1956).Google Scholar
[1]Kurosh, A. G., The theory of groups, vol. II (Chelsea, New York, 1956).Google Scholar
[2]Neumann, B. H., ‘An essay on free products of groups with amalgamations’, Phil. Trans. Roy. Soc. (A) 246 (1954), 503–554.Google Scholar
[3]Neumann, Hanna, ‘Generalized free products with amalgamated subgroups II’, Amer. J. Math. 71 (1949), 491–540.Google Scholar
[4]Dey, I. M. S., ‘Schreier systems in free products’, Proc. Glasgow Math. Assoc. 7 (1965), 61–79.CrossRefGoogle Scholar