A note on Baker's method

Extract

Let …, α_n, (n ≧ 2) be (fixed) multiplicatively independent non zero algebraic numbers and set M(H) = min |β¹log α¹+…+βⁿ log αⁿ| the minimum taken over all algebraic numbers bgr;¹,…βⁿ not all equal to zero, of degrees not exceeding a fixed natural number d₀, and heights not exceeding an arbitrary natural number H. Then an important result [1] of Baker states that 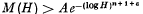for every fixed ε > 0 and an explicit constant 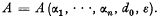. It may be remarked that Baker deduces his general result from the special case where βⁿ is fixed to be —1. The following straight forward generalization might be of some interest since it shows that the exponent n+1+ε need not be the best, and that the best exponent obtainable by his method has some chance of being 1 + ε (see the corollary to the Theorem).