Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T08:15:07.156Z Has data issue: false hasContentIssue false
  • English
  • Français

Normality of some p—adic product expansions

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  09 April 2009

Arnold Knopfmacher  and
John Knopfmacher
Arnold Knopfmacher
Affiliation:
Department of Computational andApplied Mathematics University of the WitwatersrandJohannesburg, Wits 2050, South Africa
John Knopfmacher
Affiliation:
Department of MathematicsUniversity of the Witwatersrand Johannesburg, Wits 2050, South Africa
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider two unique products 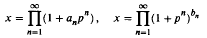for a given p—adic integer x with leading coefficient 1, where anbn ∈ {0, 1,… p − 1}. It is shown that, for almost all such x relative to Haar measure on the p—adic integers, the sequences (an), (bn) are normal to base p, and have standard normal distribution functions.

MSC classification

Secondary: 11K41: Continuous, $p$-adic and abstract analogues 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 49 , Issue 2 , October 1990 , pp. 258 - 263
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Galambos, J., Representations of real numbers by infinite series, (Springer, 1976).CrossRefGoogle Scholar
[2]Knopfmacher, A. and Knopfmacher, J., ‘A product expansion in p-adic and other nonarchimedean fields’, Proc. Amer. Math. Soc. 104 (1988), 1031–1035.Google Scholar
[3]Knopfmacher, A. and Knopfmacher, J., ‘A binomial product representation for p—adic numbers’, Arch. Math. 52 (1989), 333–336.CrossRefGoogle Scholar
[4]Kuipers, L. and Niederreiter, H., Uniform distribution of sequences, (Wiley, 1974).Google Scholar
[5]Postnikov, A. G., Ergodic problems in the theory of congruences and of diophantine approximations, (Amer. Math. Soc., 1967).Google Scholar
[6]Ruban, A. A., ‘Some metric properties of the p-adic numbers’, Siberian Math. J. 11 (1970), 176–180.CrossRefGoogle Scholar
[7]Sprindžuk, V. G., Mahler's problem in metric number theory, (Amer. Math. Soc., 1969).Google Scholar