Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T08:09:49.291Z Has data issue: false hasContentIssue false
  • English
  • Français

NORMAL CYCLIC POLYTOPES AND CYCLIC POLYTOPES THAT ARE NOT VERY AMPLE

Part of: Algebraic combinatorics Polytopes and polyhedra

Published online by Cambridge University Press:  30 September 2013

TAKAYUKI HIBI ,
AKIHIRO HIGASHITANI ,
LUKAS KATTHÄN  and
RYOTA OKAZAKI
TAKAYUKI HIBI
Affiliation:
Department of Pure and Applied Mathematics, Graduate School of Information Science and Technology, Osaka University, Toyonaka, Osaka 560-0043, Japan email [email protected]
AKIHIRO HIGASHITANI*
Affiliation:
Department of Pure and Applied Mathematics, Graduate School of Information Science and Technology, Osaka University, Toyonaka, Osaka 560-0043, Japan email [email protected]
LUKAS KATTHÄN
Affiliation:
Fachbereich Mathematik und Informatik, Philipps-Universität Marburg, 35032 Marburg, Germany email [email protected]
RYOTA OKAZAKI
Affiliation:
Faculty of Education, Fukuoka University of Education, Munakata, Fukuoka 811-4192, Japan email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 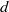$d$ and $n$ be positive integers such that 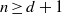$n\geq d+ 1$ and 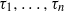${\tau }_{1} , \ldots , {\tau }_{n} $ integers such that 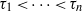${\tau }_{1} \lt \cdots \lt {\tau }_{n} $. Let 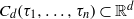${C}_{d} ({\tau }_{1} , \ldots , {\tau }_{n} )\subset { \mathbb{R} }^{d} $ denote the cyclic polytope of dimension 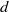$d$ with $n$ vertices 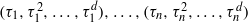$({\tau }_{1} , { \tau }_{1}^{2} , \ldots , { \tau }_{1}^{d} ), \ldots , ({\tau }_{n} , { \tau }_{n}^{2} , \ldots , { \tau }_{n}^{d} )$. We are interested in finding the smallest integer 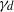${\gamma }_{d} $ such that if 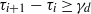${\tau }_{i+ 1} - {\tau }_{i} \geq {\gamma }_{d} $ for 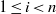$1\leq i\lt n$, then 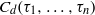${C}_{d} ({\tau }_{1} , \ldots , {\tau }_{n} )$ is normal. One of the known results is 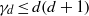${\gamma }_{d} \leq d(d+ 1)$. In the present paper a new inequality 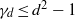${\gamma }_{d} \leq {d}^{2} - 1$ is proved. Moreover, it is shown that if 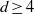$d\geq 4$ with 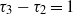${\tau }_{3} - {\tau }_{2} = 1$, then 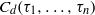${C}_{d} ({\tau }_{1} , \ldots , {\tau }_{n} )$ is not very ample.

Keywords

cyclic polytopenormal polytopevery ample polytope

MSC classification

Secondary: 52B20: Lattice polytopes (including relations with commutative algebra and algebraic geometry) 05E40: Combinatorial aspects of commutative algebra 05E45: Combinatorial aspects of simplicial complexes
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 1 , February 2014 , pp. 61 - 77
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Bruns, W. and Gubeladze, J., Polytopes, Rings and K-theory (Springer, Heidelberg, 2009).Google Scholar
Grünbaum, B., Convex Polytopes, 2nd edn (Springer, Heidelberg, 2003).Google Scholar
Gubeladze, J., ‘Convex normality of rational polytopes with long edges’, Adv. Math. 230 (2012), 372–389.Google Scholar
Hibi, T., Algebraic Combinatorics on Convex Polytopes (Carslaw Publications, Glebe, NSW, Australia, 1992).Google Scholar
Hibi, T., Higashitani, A, Katthän, L. and Okazaki, R., Toric rings arising from cyclic polytopes. arXiv:1204.5565v1.Google Scholar
Ohsugi, H. and Hibi, T., ‘Normal polytopes arising from finite graphs’, J. Algebra 207 (1998), 409–426.CrossRefGoogle Scholar
Ohsugi, H. and Hibi, T., ‘Nonvery ample configurations arising from contingency tables’, Ann. Inst. Statist. Math. 62 (2010), 639–644.Google Scholar
Schrijver, A., Theory of Linear and Integer Programming (John Wiley & Sons, Chichester, 1986).Google Scholar
Stanley, R. P., Combinatorics and Commutative Algebra, 2nd edn (Birkhäuser, Boston, 1995).Google Scholar
Ziegler, G. M., Lectures on Polytopes (Springer, Heidelberg, 1995).Google Scholar