Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lorente, M.
and
Riveros, M. S.
2005.
Two weight norm inequalities for communtators of one-sided singular integrals and the one-sided discrete square function.
Journal of the Australian Mathematical Society,
Vol. 79,
Issue. 1,
p.
77.
Wang, J.
Ren, Y.
and
Zhang, E.
2023.
A Weighted Weak-Type Inequality for One-Sided Maximal Operators.
Ukrainian Mathematical Journal,
Vol. 75,
Issue. 5,
p.
817.
Wang, J.
Ren, Y.
and
Zhang, E.
2023.
A weighted weak-type inequality for the one-sided maximal operators.
Ukrains’kyi Matematychnyi Zhurnal,
Vol. 75,
Issue. 5,
p.
712.
Lorente, María
Martín-Reyes, Francisco J.
and
Rivera-Ríos, Israel P.
2023.
One-sided estimates via function.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 153,
Issue. 6,
p.
2079.
Zhang, Erxin
and
Ren, Yanbo
2023.
A Unified Version of Weighted Weak Type Inequalities for One-Sided Maximal Function on $${\mathbb {R}}^2$$.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 4,
Ren, Yanbo
and
Wang, Jing
2024.
Criteria of a Four-Weight Weak Type Inequality for One-Sided Maximal Operators in Orlicz Classes.
Mediterranean Journal of Mathematics,
Vol. 21,
Issue. 2,
Zhang, Erxin
2024.
A Unified Version of Weighted Weak-Type Inequalities for the One-Sided Hardy–Littlewood Maximal Function in Orlicz Classes.
Mathematics,
Vol. 12,
Issue. 18,
p.
2814.


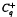 condition, then the
condition, then the 