Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T08:52:22.922Z Has data issue: false hasContentIssue false
  • English
  • Français

NONVANISHING ELEMENTS FOR BRAUER CHARACTERS

Part of: Representation theory of groups

Published online by Cambridge University Press:  13 August 2015

SILVIO DOLFI ,
EMANUELE PACIFICI  and
LUCIA SANUS
SILVIO DOLFI
Affiliation:
Dipartimento di Matematica U. Dini, Università degli Studi di Firenze, viale Morgagni 67/a, 50134 Firenze, Italy email [email protected]
EMANUELE PACIFICI*
Affiliation:
Dipartimento di Matematica F. Enriques, Università degli Studi di Milano, via Saldini 50, 20133 Milano, Italy email [email protected]
LUCIA SANUS
Affiliation:
Departament d’Àlgebra, Facultat de Matemàtiques, Universitat de València, 46100 Burjassot, València, Spain email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 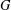$G$ be a finite group and 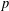$p$ a prime. We say that a 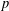$p$-regular element 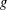$g$ of 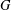$G$ is 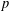$p$-nonvanishing if no irreducible 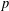$p$-Brauer character of 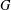$G$ takes the value 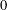$0$ on 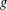$g$. The main result of this paper shows that if 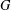$G$ is solvable and 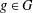$g\in G$ is a 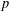$p$-regular element which is 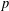$p$-nonvanishing, then 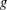$g$ lies in a normal subgroup of 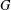$G$ whose $p$-length and 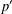$p^{\prime }$-length are both at most 2 (with possible exceptions for 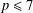$p\leq 7$), the bound being best possible. This result is obtained through the analysis of one particular orbit condition in linear actions of solvable groups on finite vector spaces, and it generalizes (for 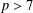$p>7$) some results in Dolfi and Pacifici [‘Zeros of Brauer characters and linear actions of finite groups’, J. Algebra 340 (2011), 104–113].

Keywords

finite groupsBrauer characters

MSC classification

Primary: 20C20: Modular representations and characters
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 1 , February 2017 , pp. 96 - 107
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Dolfi, S., ‘Orbits of permutation groups on the power set’, Arch. Math. 75 (2000), 321–327.Google Scholar
Dolfi, S., ‘Large orbits in coprime actions of solvable groups’, Trans. Amer. Math. Soc. 360 (2008), 135–152.Google Scholar
Dolfi, S., Navarro, G., Pacifici, E., Sanus, L. and Tiep, P. H., ‘Non-vanishing elements of finite groups’, J. Algebra 323 (2010), 540–545.Google Scholar
Dolfi, S. and Pacifici, E., ‘Zeros of Brauer characters and linear actions of finite groups’, J. Algebra 340 (2011), 104–113.Google Scholar
Foulser, D., ‘Solvable primitive permutation groups of low rank’, Trans. Amer. Math. Soc. 143 (1969), 1–54.Google Scholar
Isaacs, I. M., Navarro, G. and Wolf, T. R., ‘Finite group elements where no irreducible character vanishes’, J. Algebra 222 (1999), 413–423.CrossRefGoogle Scholar
Manz, O. and Wolf, T. R., Representations of Solvable Groups (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Navarro, G., Characters and Blocks of Finite Groups (Cambridge University Press, Cambridge, 1998).Google Scholar
Seress, A., ‘The minimal base size of primitive solvable permutation groups’, J. Lond. Math. Soc. (2) 53 (1996), 243–255.Google Scholar
Yang, Y., ‘Regular orbits of finite primitive solvable groups, II’, J. Algebra 341 (2011), 23–34.CrossRefGoogle Scholar