Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T07:55:21.538Z Has data issue: false hasContentIssue false
  • English
  • Français

NONORTHOGONAL GEOMETRIC REALIZATIONS OF COXETER GROUPS

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  25 July 2014

XIANG FU
XIANG FU*
Affiliation:
School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define in an axiomatic fashion a Coxeter datum for an arbitrary Coxeter group 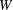$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}W$. This Coxeter datum will specify a pair of reflection representations of 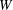$W$ in two vector spaces linked only by a bilinear pairing without any integrality or nondegeneracy requirements. These representations are not required to be embeddings of 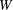$W$ in the orthogonal group of any vector space, and they give rise to a pair of inter-related root systems generalizing the classical root systems of Coxeter groups. We obtain comparison results between these nonorthogonal root systems and the classical root systems. Further, we study the equivalent of the Tits cone in these nonorthogonal representations.

Keywords

Coxeter groupsKac–Moody Lie algebrasroot systemsTits cone

MSC classification

Secondary: 20F55: Reflection and Coxeter groups 20F10: Word problems, other decision problems, connections with logic and automata 20F65: Geometric group theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 2 , October 2014 , pp. 180 - 211
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Bourbaki, N., Groupes et algebras de Lie, Chapitres 4, 5 et 6 (Hermann, Paris) (in French).Google Scholar
Brink, B. and Howlett, R. B., ‘A finiteness property and an automatic structure of Coxeter groups’, Math. Ann. 296 (1993), 179–190.CrossRefGoogle Scholar
Brink, B., ‘The set of dominance-minimal roots’, J. Algebra 206 (1998), 371–412.CrossRefGoogle Scholar
Bergeron, F., Bergeron, N., Howlett, R. B. and Taylor, D. E., ‘A decomposition of the descent algebra of a finite Coxeter group’, J. Algebraic Combin. 1 (1992), 23–44.CrossRefGoogle Scholar
Casselman, W. A., ‘Computation in Coxeter groups I. Multiplication’, Electron. J. Combin. 9(1) (2002), Research Paper 25, 22 pp. (electronic).CrossRefGoogle Scholar
Casselman, W. A., ‘Computation in Coxeter groups II. Constructing minimal roots’, Represent. Theory 12 (2008), 260–293.CrossRefGoogle Scholar
Caprace, P. E. and Rémy, B., ‘Groups with a root group datum’, Innov. Incidence Geom. 9 (2009), 5–77.CrossRefGoogle Scholar
Dyer, M., ‘Imaginary cone and reflection subgroups of Coxeter groups’, Preprint, 2012,arXiv:1210.5206.Google Scholar
Dyer, M., Hohlweg, C. and Ripoll, V., ‘Imaginary cones and limit roots of infinite Coxeter groups’, Preprint, 2013, arXiv:1303.6710.Google Scholar
Fu, X., ‘Root systems and reflection representations of Coxeter groups’, PhD Thesis, University of Sydney, 2010.Google Scholar
Fu, X., ‘The dominance hierarchy in root systems of Coxeter groups’, J. Algebra 366 (2012), 187–204.CrossRefGoogle Scholar
Hée, J.-Y., ‘Le cône imaginaire d’une base de racines sur $\mathbb{R}$’, private communication, 2013.Google Scholar
Hée, J.-Y., ‘Systèmes de racines sur un anneau commutatif totalement ordonné’, Geom. Dedicata 37 (1991), 65–102.CrossRefGoogle Scholar
Hée, J. Y., ‘Sur la torsion de Steinberg-Ree des groupes de Chevalley et des groupes de Kac–Moody’, Thèse d’ État de l’ Université Paris XI, Orsay, 1993.Google Scholar
Hée, J. Y., ‘Générateurs de racines’, private communication, 2013.Google Scholar
Hiller, H., Geometry of Coxeter Groups, Research Notes in Mathematics, 54 (Pitman, Boston, 1981).Google Scholar
Hohlweg, C., Labbé, J. P. and Ripoll, V., ‘Asymptotical behaviour of roots of infinite Coxeter groups I’, Canad. J. Math. 66(2) (2014), 323–353.CrossRefGoogle Scholar
Howlett, R. B., ‘Introduction to Coxeter groups’, in: Lectures given at ANU (1996), available athttp://www.maths.usyd.edu.au/res/Algebra/How/1997-6.html.Google Scholar
Howlett, R. B., Rowley, P. J. and Taylor, D. E., ‘On outer automorphism groups of Coxeter groups’, Manuscripta Math. 93 (1997), 499–513.CrossRefGoogle Scholar
Humphreys, J., Reflection Groups and Coxeter Groups, Cambridge Studies in Advanced Mathematics, 29 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Kac, V. G., Infinite-dimensional Lie Algebras, 3rd edn (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Krammer, D., ‘The conjugacy problem for Coxeter groups’, PhD Thesis, Universiteit Utrecht, 1994.Google Scholar
Krammer, D., ‘The conjugacy problem for Coxeter groups’, Groups Geom. Dyn. 3(1) (2009), 71–171.CrossRefGoogle Scholar
Maxwell, G. A., ‘Sphere packings and hyperbolic reflection groups’, J. Algebra 79 (1982), 78–97.CrossRefGoogle Scholar
Moody, R. V. and Pianzola, A., ‘On infinite root systems’, Trans. Amer. Math. Soc. 315 (1989), 661–696.CrossRefGoogle Scholar
Vinberg, È. B., ‘Discrete linear groups generated by reflections’, Izv. Akad. Nauk SSSR Ser. Mat. 35 (1971), 1072–1112.Google Scholar
Witt, E., ‘Spiegelungsgruppen und Aufzählung halbeinfacher Liescher Ringe’, Abh. Math. Sem. Hansischen Univ. 14 (1941), 289–322.CrossRefGoogle Scholar