Published online by Cambridge University Press: 09 April 2009
A (ν, κ, λ)-graph is defined in [3] as a graph on ν points, each of valency κ, and such that for any two points P and Q there are exactly λ points which are joined to both. In other words, if Si is the set of points joined to Pi, then
Si has k elements for any i
Si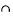 Sj has λ elements if i≠j
Sj has λ elements if i≠j
The sets Si are the blocks of a (v, k, λ)-configuration, so a necessary condition on v, k, and λ that a graph should exist is that a (v, k, λ)- configuration should exist. Another necessary condition, reported by Bose (see [1]) and others, is that there should be an integer m satisfying 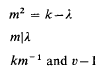 have equal parity. We shall prove that these conditions are not sufficient.
have equal parity. We shall prove that these conditions are not sufficient.