Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T08:39:37.555Z Has data issue: false hasContentIssue false
  • English
  • Français

NILPOTENCY IN UNCOUNTABLE GROUPS

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  27 October 2016

FRANCESCO DE GIOVANNI  and
MARCO TROMBETTI
FRANCESCO DE GIOVANNI*
Affiliation:
Dip. di Matematica e Appl., Università di Napoli Federico II, Via Cintia, Napoli, Italy email [email protected]
MARCO TROMBETTI
Affiliation:
Dip. di Matematica e Appl., Università di Napoli Federico II, Via Cintia, Napoli, Italy email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main purpose of this paper is to investigate the behaviour of uncountable groups of cardinality 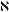$\aleph$ in which all proper subgroups of cardinality 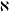$\aleph$ are nilpotent. It is proved that such a group 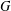$G$ is nilpotent, provided that 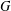$G$ has no infinite simple homomorphic images and either 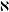$\aleph$ has cofinality strictly larger than 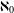$\aleph _{0}$ or the generalized continuum hypothesis is assumed to hold. Furthermore, groups whose proper subgroups of large cardinality are soluble are studied in the last part of the paper.

Keywords

uncountable groupnilpotent groupsoluble group

MSC classification

Primary: 20F18: Nilpotent groups
Secondary: 20F19: Generalizations of solvable and nilpotent groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 1 , August 2017 , pp. 59 - 69
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors are members of GNSAGA-INdAM, and this work was carried out within the ADV-AGTA project.

References

Baer, R., ‘Überauflösbare Gruppen’, Abh. Math. Semin. Univ. Hambg. 23 (1959), 11–28.Google Scholar
De Falco, M., de Giovanni, F. and Musella, C., ‘Large soluble groups and the control of embedding properties’, Ricerche Mat. 63(suppl. 1) (2014), 117–130.CrossRefGoogle Scholar
Dixon, M. R., Evans, M. J. and Smith, H., ‘Locally (soluble-by-finite) groups with all proper insoluble subgroups of finite rank’, Arch. Math. (Basel) 68 (1997), 100–109.CrossRefGoogle Scholar
Doerk, K., ‘Minimal nicht-überauflösbare, endliche Gruppen’, Math. Z. 91 (1966), 198–205.Google Scholar
de Giovanni, F. and Trombetti, M., ‘Infinite minimal non-hypercyclic groups’, J. Algebra Appl. 14(10) (2015), 15 pages, doi:10.1142/S0219498815501431.Google Scholar
de Giovanni, F. and Trombetti, M., ‘Uncountable groups with restrictions on subgroups of large cardinality’, J. Algebra 447 (2016), 383–396.Google Scholar
Jech, T., Set Theory – The Third Millennium Edition (Springer, Berlin, 2003).Google Scholar
Kuroš, A. G. and Černikov, S. N., ‘Solvable and nilpotent groups’, Uspekhi Mat. Nauk (N.S.) 2 (1947), 18–59; Amer. Math. Soc. Translations 80 (1953).Google Scholar
Lennox, J. C. and Robinson, D. J. S., The Theory of Infinite Soluble Groups (Clarendon Press, Oxford, 2004).Google Scholar
Longobardi, P., Maj, M. and Smith, H., ‘A note on locally graded groups’, Rend. Semin. Mat. Univ. Padova 94 (1995), 275–277.Google Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups (Springer, Berlin, 1972).Google Scholar
Shelah, S., ‘On a problem of Kurosh, Jónsson groups, and applications’, in: Word Problems II – the Oxford Book (North-Holland, Amsterdam, 1980), 373–394.Google Scholar