Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T08:14:45.108Z Has data issue: false hasContentIssue false
  • English
  • Français

MODULES OVER ÉTALE GROUPOID ALGEBRAS AS SHEAVES

Part of: Categories and geometry Topological and differentiable algebraic systems Rings and algebras arising under various constructions

Published online by Cambridge University Press:  09 September 2014

BENJAMIN STEINBERG
BENJAMIN STEINBERG*
Affiliation:
Department of Mathematics, City College of New York, Convent Avenue at 138th Street, NY, New York 10031, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

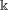The author has previously associated to each commutative ring with unit $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\Bbbk $ and étale groupoid 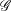$\mathscr{G}$ with locally compact, Hausdorff, totally disconnected unit space a 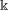$\Bbbk $-algebra 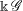$\Bbbk \, \mathscr{G}$. The algebra 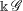$\Bbbk \, \mathscr{G}$ need not be unital, but it always has local units. The class of groupoid algebras includes group algebras, inverse semigroup algebras and Leavitt path algebras. In this paper we show that the category of unitary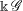$\Bbbk \, \mathscr{G}$-modules is equivalent to the category of sheaves of 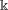$\Bbbk $-modules over 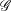$\mathscr{G}$. As a consequence, we obtain a new proof of a recent result that Morita equivalent groupoids have Morita equivalent algebras.

Keywords

étale groupoidsgroupoid algebrassheaves

MSC classification

Secondary: 16S99: None of the above, but in this section 16S10: Rings determined by universal properties (free algebras, coproducts, adjunction of inverses, etc.) 22A22: Topological groupoids (including differentiable and Lie groupoids) 18F20: Presheaves and sheaves
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 3 , December 2014 , pp. 418 - 429
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Abrams, G. D., ‘Morita equivalence for rings with local units’, Comm. Algebra 11(8) (1983), 801–837.Google Scholar
Abrams, G. D. and Aranda-Pino, G., ‘The Leavitt path algebras of arbitrary graphs’, Houston J. Math. 34 (2008), 423–442.Google Scholar
Anh, P. N. and Marki, L., ‘Morita equivalence for rings without identity’, Tsukuba J. Math. 11(1) (1987), 1–16.Google Scholar
Brown, J., Clark, L. O., Farthing, C. and Sims, A., ‘Simplicity of algebras associated to étale groupoids’, Semigroup Forum 88(2) (2014), 433–452.Google Scholar
Clark, L. O. and Edie-Michell, C., ‘Uniqueness theorems for Steinberg algebras’, 2014, http://arxiv.org/abs/1403.4684.Google Scholar
Clark, L. O., Farthing, C., Sims, A. and Tomforde, M., ‘A groupoid generalisation of Leavitt path algebras’, Semigroup Forum (to appear).Google Scholar
Clark, L. O. and Sims, A., ‘Equivalent groupoids have Morita equivalent Steinberg algebras’, 2013, http://arxiv.org/abs/1311.3701.Google Scholar
Crainic, M. and Moerdijk, I., ‘A homology theory for étale groupoids’, J. reine angew. Math. 521 (2000), 25–46.Google Scholar
Exel, R., ‘Inverse semigroups and combinatorial C ∗-algebras’, Bull. Braz. Math. Soc. (N.S.) 39(2) (2008), 191–313.Google Scholar
García, J. L. and Simón, J. J., ‘Morita equivalence for idempotent rings’, J. Pure Appl. Algebra 76(1) (1991), 39–56.Google Scholar
Johnstone, P. T., Sketches of an Elephant: A Topos Theory Compendium. Vol. 1, Oxford Logic Guides, 43 (Clarendon Press and Oxford University Press, New York, 2002).Google Scholar
Johnstone, P. T., Sketches of an Elephant: A Topos Theory Compendium. Vol. 2, Oxford Logic Guides, 44 (Clarendon Press and Oxford University Press, Oxford, 2002).Google Scholar
Kališnik, J., ‘Representations of étale Lie groupoids and modules over Hopf algebroids’, Czechoslovak Math. J. 61(3) (2011), 653–672.Google Scholar
Lawson, M. V., Inverse Semigroups, The Theory of Partial Symmetries (World Scientific, River Edge, NJ, 1998).Google Scholar
Mitchell, B., ‘Rings with several objects’, Adv. Math. 8 (1972), 1–161.Google Scholar
Moerdijk, I., ‘The classifying topos of a continuous groupoid. I’, Trans. Amer. Math. Soc. 310(2) (1988), 629–668.CrossRefGoogle Scholar
Moerdijk, I., ‘Toposes and groupoids’, in: Categorical Algebra and its Applications (Louvain-La-Neuve, 1987), Lecture Notes in Mathematics, 1348 (Springer, Berlin, 1988), 280–298.CrossRefGoogle Scholar
Moerdijk, I., ‘The classifying topos of a continuous groupoid. II’, Cah. Topol. Géom. Différ. Catég. 31(2) (1990), 137–168.Google Scholar
Mrcun, J., ‘Stability and invariants of Hilsum–Skandalis maps’, PhD Thesis, Utrecht University, 1996, http:/arxiv:org/abs/math/0506484 (2005).Google Scholar
Paterson, A. L. T., Groupoids, Inverse Semigroups, and their Operator Algebras, Progress in Mathematics, 170 (Birkhäuser, Boston, MA, 1999).Google Scholar
Pierce, R. S., ‘Modules over commutative regular rings’, Mem. Amer. Math. Soc. 70 (1967).Google Scholar
Renault, J., A Groupoid Approach to C ∗-algebras, Lecture Notes in Mathematics, 793 (Springer, Berlin, 1980).Google Scholar
Renault, J., ‘Représentation des produits croisés d’algèbres de groupoïdes’, J. Operator Theory 18(1) (1987), 67–97.Google Scholar
Resende, P., ‘Étale groupoids and their quantales’, Adv. Math. 208(1) (2007), 147–209.Google Scholar
Steinberg, B., ‘A groupoid approach to discrete inverse semigroup algebras’, 2009, http://arxiv.org/abs/0903.3456.Google Scholar
Steinberg, B., ‘A groupoid approach to discrete inverse semigroup algebras’, Adv. Math. 223(2) (2010), 689–727.Google Scholar