Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-18T10:49:28.684Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimum sized fibres in distributive lattices

Part of: Boolean algebras (Boolean rings) Distributive lattices Ordered sets

Published online by Cambridge University Press:  09 April 2009

Dwight Duffus  and
Bill Sands
Dwight Duffus
Affiliation:
Mathematics and Computer Science Department Emory UniversityAtlanta GA 30322USA e-mail: [email protected]
Bill Sands
Affiliation:
Mathematics and Statistics Department The University of CalgaryCalgary AB T2N 1N4Canada e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subset F of an ordered set X is a fibre of X if F intersects every maximal antichain of X. We find a lower bound on the function ƒ (D), the minimum fibre size in the distributive lattice D, in terms of the size of D. In particular, we prove that there is a constant c such that 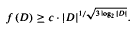In the process we show that minimum fibre size is a monotone property for a certain class of distributive lattices. This fact depends upon being able to split every maximal antichain of this class of distributive lattices into two parts so that the lattice is the union of the upset of one part and the downset of the other.

Keywords

distributive latticefibremaximal antichainsplitting property

MSC classification

Secondary: 06A07: Combinatorics of partially ordered sets 06D99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 70 , Issue 3 , June 2001 , pp. 337 - 350
Copyright
Copyright © Australian Mathematical Society 2001

References

[1]Ahlswede, R., Erdős, P. L., and Graham, N., ‘A splitting property of maximal antichains’, Combinatorica 15 (1995), 475–480.Google Scholar
[2]Aigner, M. and Andreae, T., ‘Vertex sets that meet all maximal cliques of a graph’, preprint (1986).Google Scholar
[3]Bajnok, B., ‘On the minimum width of a cutset in the truncated Boolean lattice’, Congr. Numer. 130 (1998), 77–81.Google Scholar
[4]Bajnok, B. and Shahriari, S., ‘Long symmetric chains in the Boolean lattice’, J. Combin. Theory Ser. A 75 (1996), 44–54.Google Scholar
[5]Duffus, D. and Sands, B., ‘Finite distributive lattices with the splitting property’, in preparation.Google Scholar
[6]Duffus, D., Sands, B., and Winkler, P., ‘Maximal chains and antichains in Boolean lattices’, SIAM J. Disc. Math. 3 (1990), 197–205.Google Scholar
[7]Džamonja, M., ‘A note on the splitting property in strongly dense posets of size ℵ0’, Radovi Matematički 8 (1999), 321–326.Google Scholar
[8]Erdős, P. L., ‘Splitting property in infinite posets’, Discrete Math. 163 (1997), 251–256.Google Scholar
[9]Faigle, U. and Sands, B., ‘A size-width inequality for distributive lattices’, Combinatorica 6 (1986), 29–33.Google Scholar
[10]Füredi, Z., Griggs, J., and Kleitman, D., ‘A minimal cutset of the Boolean lattice with almost all members’, Graphs Combin. 5 (1989), 327–333.Google Scholar
[11]Kahn, J. and Saks, M., ‘On the widths of finite distributive lattices’, Discrete Math. 63 (1987), 183–195.CrossRefGoogle Scholar
[12]Lonc, Z. and Rival, I., ‘Chains, antichains and fibres’, J. Combin. Theory Ser. A 44 (1987), 207–228.Google Scholar
[13]Łuczak, T., private communication, 03 1998.Google Scholar