Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T07:34:12.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimum determinant of asymmetric quadratic forms

Published online by Cambridge University Press:  09 April 2009

R. T. Worley
R. T. Worley
Affiliation:
The University of AdelaideAdelaide, S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f = f (x1, x2,… xn) be an indefinite n-ary quadratic form of signature s and let m+(f), m−(f) denote the infimum of the non-negative values taken by f and —f respectively for integral (x1, x2,…, xn) ≠ (0, 0,…, 0). Furthermore let f satisfy the condition m+ (f) ≠ 0 and let 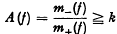for some integer k. Then Segré [3] has shown that, for n = 2, f must have determinant det (f) satisfying 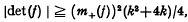with equality if and only if f is equivalent under an integral unimodular transformation (denoted ˜) to a multiple of the form f1(x, y) = x2−kxy−ky2, while Oppenheim [2] has shown that, for n ≧ 3, 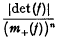is of the order of k2n−2

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 7 , Issue 2 , May 1967 , pp. 177 - 190
Copyright
Copyright © Australian Mathematical Society 1967

References

[1]Dickson, L. E., Introduction to the theory of numbers (University of Chicago Press, 1929).Google Scholar
[2]Oppenheim, A., ‘Value of quadratic forms’, Quart. J. Math. Oxford (2) 4 (1953), 54–59.CrossRefGoogle Scholar
[3]Segré, M. B., ‘Lattice Points in infinite domains and asymmetric diophantine approximations’, Duke Math. J. 12 (1945), 337–365.Google Scholar
[4]Tornheim, L., ‘Asymmetric minima of quadratic forms and asymmetric diophantine approximation’, Duke Math. J. 22 (1955), 287–294.Google Scholar