Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T14:11:05.419Z Has data issue: false hasContentIssue false
  • English
  • Français

MINIMAL VOLUME OF COMPLETE UNIFORM VISIBILITY MANIFOLDS WITH FINITE VOLUME

Part of: Special aspects of infinite or finite groups Global differential geometry

Published online by Cambridge University Press:  07 June 2013

SUNGWOON KIM
SUNGWOON KIM*
Affiliation:
School of Mathematics, Korea Institute for Advanced Science, Hoegiro 85, Dongdaemun-gu, Seoul, 130-722, Republic of Korea email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that complete uniform visibility manifolds of finite volume with sectional curvature 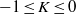$- 1\leq K\leq 0$ have positive simplicial volume. This implies that their minimal volume is nonzero.

Keywords

minimal volumesimplicial volumevisibility manifold

MSC classification

Secondary: 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces 20F67: Hyperbolic groups and nonpositively curved groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 94 , Issue 3 , June 2013 , pp. 375 - 384
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Bowditch, B. H., ‘Relatively hyperbolic groups’, Internat. J. Algebra Comput. 22 (3) (2012), 1250016, 66 pages.CrossRefGoogle Scholar
Bridson, M. R., ‘On the existence of flat planes in spaces of nonpositive curvature’, Proc. Amer. Math. Soc. 123 (1) (1995), 223–235.Google Scholar
Cao, J. and Chen, X., ‘Minimal volume and simplicial norm of visibility $n$-manifolds and compact 3-manifolds’, arXiv:0812.3353 [math.DG].Google Scholar
Dahmani, F. and Yaman, A., ‘Bounded geometry in relatively hyperbolic groups’, New York J. Math. 11 (2005), 89–95.Google Scholar
Eberlein, P., ‘Lattices in spaces of nonpositive curvature’, Ann. of Math. (2) 111 (3) (1980), 435–476.CrossRefGoogle Scholar
Eberlein, P. and O’Neill, B., ‘Visibility manifolds’, Pacific J. Math. 46 (1973), 45–109.CrossRefGoogle Scholar
Farb, B., ‘Relatively hyperbolic groups’, Geom. Funct. Anal. 8 (5) (1998), 810–840.CrossRefGoogle Scholar
Gromov, M., ‘Volume and bounded cohomology’, Publ. Math. Inst. Hautes Études Sci. 56 (1982), 5–99.Google Scholar
Gromov, M., ‘Hyperbolic groups’, in: Essays in Group Theory, Mathematical Sciences Research Institute Publications, 8 (Springer, New York, 1987), 75–263.CrossRefGoogle Scholar
Kim, S. and Kim, I., ‘Simplicial volume of $ \mathbb{Q} $-rank one locally symmetric spaces covered by the product of $ \mathbb{R} $-rank one symmetric spaces’, Algebr. Geom. Topol. 12 (2) (2012), 1165–1181.CrossRefGoogle Scholar
Lafont, J. and Schmidt, B., ‘Simplicial volume of closed locally symmetric spaces of noncompact type’, Acta Math. 197 (1) (2006), 129–143.CrossRefGoogle Scholar
Löh, C., ‘Isomorphisms in ${\ell }^{1} $-homology’, Münster J. Math. 1 (2008), 237–265.Google Scholar
Löh, C. and Sauer, R., ‘Degree theorems and Lipschitz simplicial volume for nonpositively curved manifolds of finite volume’, J. Topol. 2 (1) (2009), 193–225.CrossRefGoogle Scholar
Löh, C. and Sauer, R., ‘Simplicial volume of hilbert modular varieties’, Comment. Math. Helv. 84 (3) (2009), 457–470.CrossRefGoogle Scholar
Mineyev, I. and Yaman, A., ‘Relative hyperbolicity and bounded cohomology’, online at http://www.math.uiuc.edu/~mineyev/math/art/rel-hyp.pdf.Google Scholar
Phan, T. T. N., ‘On finite volume, negatively curved manifolds’, arXiv:1110.4087 [math.DG].Google Scholar
Thurston, W., ‘Geometry and topology of 3-manifolds’, Princeton University Lecture Notes (1982), online at http://library.msri.org/books/gt3m.Google Scholar