THE MEAN CURVATURE EQUATION ON SEMIDIRECT PRODUCTS 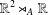$\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$: HEIGHT ESTIMATES AND SCHERK-LIKE GRAPHS

Abstract

In the ambient space of a semidirect product 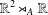$\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$, we consider a connected domain 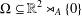${\rm\Omega}\subseteq \mathbb{R}^{2}\rtimes _{A}\{0\}$. Given a function 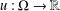$u:{\rm\Omega}\rightarrow \mathbb{R}$, its ${\it\pi}$-graph is 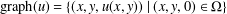$\text{graph}(u)=\{(x,y,u(x,y))\mid (x,y,0)\in {\rm\Omega}\}$. In this paper we study the partial differential equation that $u$ must satisfy so that 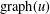$\text{graph}(u)$ has prescribed mean curvature 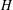$H$. Using techniques from quasilinear elliptic equations we prove that if a ${\it\pi}$-graph has a nonnegative mean curvature function, then it satisfies some uniform height estimates that depend on 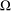${\rm\Omega}$ and on the supremum the function attains on the boundary of 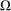${\rm\Omega}$. When 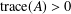$\text{trace}(A)>0$, we prove that the oscillation of a minimal graph, assuming the same constant value $n$ along the boundary, tends to zero when 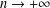$n\rightarrow +\infty$ and goes to 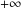$+\infty$ if 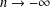$n\rightarrow -\infty$. Furthermore, we use these estimates, allied with techniques from Killing graphs, to prove the existence of minimal ${\it\pi}$-graphs assuming the value zero along a piecewise smooth curve ${\it\gamma}$ with endpoints 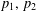$p_{1},\,p_{2}$ and having as boundary 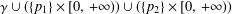${\it\gamma}\cup (\{p_{1}\}\times [0,\,+\infty ))\cup (\{p_{2}\}\times [0,\,+\infty ))$.