Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T08:53:56.831Z Has data issue: false hasContentIssue false
  • English
  • Français

Matroids whose ground sets are domains of functions

Part of: Designs and configurations

Published online by Cambridge University Press:  09 April 2009

James Oxley ,
Kevin Prendergast  and
Don Row
James Oxley
Affiliation:
Mathematics Department, IAS, Australian National University, Canberram, Australia
Kevin Prendergast
Affiliation:
Hydro Electric Commission, Hobart, Australia
Don Row
Affiliation:
Mathematics Department, University of Tasmania, Hobart, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

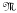From an integer-valued function f we obtain, in a natural way, a matroid Mf on the domain of f. We show that the class of matroids so obtained is closed under restriction, contraction, duality, truncation and elongation, but not under direct sum. We give an excluded-minor characterization of 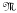and show that 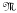consists precisely of those transversal matroids with a presentation in which the sets in the presentation are nested. Finally, we show that on an n-set there are exactly 2n members of .

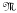MSC classification

Secondary: 05B35: Matroids, geometric lattices
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 32 , Issue 3 , June 1982 , pp. 380 - 387
Copyright
Copyright © Australian Mathematical Society 1982

References

Crapo, H. H. and Rota, G.-C. (1970), On the foundations of combinatorial theory: combinatorial geometries (M.I.T. Press, Cambridge, Massachusetts).Google Scholar
Welsh, D. J. A. (1969), ‘A bound for the number of matroids’, J. Combinatorial Theory 6, 313–316.CrossRefGoogle Scholar
Welsh, D. J. A. (1976), Matroid theory (Academic Press, London).Google Scholar