Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T09:17:29.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Major arcs in the four cubes problem

Published online by Cambridge University Press:  09 April 2009

George Szekeres
George Szekeres
Affiliation:
The University of New South WalesKensington, N.S.W. 2033, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There is an old conjecture that every integer can be decomposed into four (positive or negative) perfect cubes. More specifically one would like to know the asymptotic number of solutions of 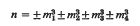when a large bound N is placed on the parts mi. Using the circle method it is shown that the number of such representations of n when N → ∞ is asymptotically equal to C(n). N for a certain positive constant C(n), provided that the contribution of the minor arcs can be neglected.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 25 , Issue 4 , June 1978 , pp. 423 - 437
Copyright
Copyright © Australian Mathematical Society 1978

References

Barrucand, P. (1960), “Sommes de Gauss et séries singulières de Hardy pour les cubes”, C. R. Acad. Sci. Paris 250, 4249–4251.Google Scholar
Fuchs, W. H. J. and Wright, E. M. (1939), “The easier Waring problem”, Quart. J. Math. Oxford Ser. 10, 190–209.CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M. (1938), An Introduction to the Theory of Numbers, 4th ed. (Oxford University Press).Google Scholar
Hasse, H. (1964), Vorlesungen über Zahlentheorie, 2nd ed. (Springer, Berlin).CrossRefGoogle Scholar
Hunter, W. (1941), “The representation of numbers by sums of fourth powers”, J. London Math. Soc. 16, 177–179.Google Scholar
Landau, E. (1927), Vorlesungen über Zahlentheorie (Chelsea, New York).Google Scholar
Mordell, L. J. (1936), “On the four integer cubes problem”, J. London Math. Soc. 11, 208–218.CrossRefGoogle Scholar
Richmond, H. W. (1922), “An elementary note upon Waring's problem for cubes, positive or negative”, Messenger Math. 51, 177–186.Google Scholar
Schinzel, A. and Sierpinski, W. (1958), “Sur les sommes de quatre cubes”, Acta Arithm. 4, 20–30.CrossRefGoogle Scholar
Wright, E. M. (1934), “An easier Waring's problem”, J. London Math. Soc. 9, 267–272.CrossRefGoogle Scholar