Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-08T21:39:06.529Z Has data issue: false hasContentIssue false
  • English
  • Français

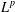$L^{p}$ BOUNDS FOR NONISOTROPIC MARCINKIEWICZ INTEGRALS ASSOCIATED TO SURFACES

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  17 August 2015

FENG LIU  and
SUZHEN MAO
FENG LIU
Affiliation:
College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, Shandong 266590, China email [email protected]
SUZHEN MAO*
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen, Fujian 361005, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

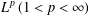In an extrapolation argument, we prove certain $L^{p}\,(1<p<\infty )$ estimates for nonisotropic Marcinkiewicz operators associated to surfaces under the integral kernels given by the elliptic sphere functions 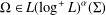${\rm\Omega}\in L(\log ^{+}L)^{{\it\alpha}}({\rm\Sigma})$ and the radial function 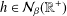$h\in {\mathcal{N}}_{{\it\beta}}(\mathbb{R}^{+})$. As applications, the corresponding results for parametric Marcinkiewicz integral operators related to area integrals and Littlewood–Paley 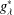$g_{{\it\lambda}}^{\ast }$-functions are given.

Keywords

nonisotropic dilationsMarcinkiewicz integralsrough kernelsextrapolation

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 42B25: Maximal functions, Littlewood-Paley theory 42B99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 3 , December 2015 , pp. 380 - 398
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Al-Qassem, H. and Pan, Y., ‘On certain estimates for Marcinkiewicz integrals and extrapolation’, Collect. Math. 60 (2009), 123–145.CrossRefGoogle Scholar
Al-Salman, A., ‘A note on parabolic Marcinkiewicz integrals along surfaces’, Proc. A. Razmadze Math. Inst. 27 (2010), 21–36.Google Scholar
Al-Salman, A., ‘Parabolic Marcinkiewicz integrals along surfaces on product domains’, Acta Math. Sin. (Engl. Ser.) 27 (2011), 1–18.CrossRefGoogle Scholar
Al-Salman, A., Al-Qassem, H., Cheng, L. C. and Pan, Y., ‘L p bounds for the function of Marcinkiewicz’, Math. Res. Lett. 9 (2002), 697–700.Google Scholar
Calderón, A. P. and Torchinsky, A., ‘On singular integrals’, Amer. J. Math. 78 (1956), 289–309.CrossRefGoogle Scholar
Chen, Y. and Ding, Y., ‘L p bounds for parabolic Marcinkiewicz integral with rough kernels’, J. Korean Math. Soc. 44 (2007), 733–745.CrossRefGoogle Scholar
Chen, Y. and Ding, Y., ‘The parabolic Littlewood–Paley operator with Hardy space kernels’, Canad. Math. Bull. 52 (2009), 521–534.CrossRefGoogle Scholar
Ding, Y., Fan, D. and Pan, Y., ‘L p -boundedness of Marcinkiewicz integrals with Hardy space function kernel’, Acta Math. Sin. (Engl. Ser.) 16 (2000), 593–600.CrossRefGoogle Scholar
Ding, Y., Fan, D. and Pan, Y., ‘On the L p boundedness of Marcinkiewicz integrals’, Michigan Math. J. 50 (2002), 17–26.CrossRefGoogle Scholar
Ding, Y., Lu, S. and Yabuta, K., ‘A problem on rough parametric Marcinkiewicz functions’, J. Aust. Math. Soc. 72 (2002), 13–21.CrossRefGoogle Scholar
Ding, Y., Xue, Q. and Yabuta, K., ‘Boundedness of the Marcinkiewicz integrals with rough kernel associated to surfaces’, Tohoku Math. J. (2) 62 (2010), 233–262.CrossRefGoogle Scholar
Duoandikoetxea, J. and Rubio de Francia, J. L., ‘Maximal and singular integral operators via Fourier transform estimates’, Invent. Math. 84 (1986), 541–561.CrossRefGoogle Scholar
Liu, F. and Wu, H., ‘On Marcinkiewicz integrals associated to compound mappings with rough kernels’, Acta Math. Sin. (Engl. Ser.) 30 (2014), 1210–1230.CrossRefGoogle Scholar
Liu, F., Wu, H. and Zhang, D., ‘L p bounds for parametric Marcinkiewicz integrals with mixed homogeneity’, Math. Inequal. Appl. 18 (2015), 453–469.Google Scholar
Liu, F. and Zhang, D., ‘Parabolic Marcinkiewicz integrals associated to polynomials, compound curves and extrapolation’, Bull. Korean Math. Soc. 52 (2015), 771–788.CrossRefGoogle Scholar
Riviére, N., ‘Singular integrals and multiplier operators’, Ark. Mat. 9 (1971), 243–278.CrossRefGoogle Scholar
Sato, S., ‘Estimates for singular integrals along surfaces of revolution’, J. Aust. Math. Soc. 86 (2009), 413–430.CrossRefGoogle Scholar
Sato, S., ‘Estimates for singular integrals and extrapolation’, Studia Math. 192 (2009), 219–233.CrossRefGoogle Scholar
Stein, E. M. and Wainger, S., ‘Problems in harmonic analysis related to curvature’, Bull. Amer. Math. Soc. (N.S.) 84 (1978), 1239–1295.CrossRefGoogle Scholar
Walsh, T., ‘On the function of Marcinkiewicz’, Studia Math. 44 (1972), 203–217.CrossRefGoogle Scholar
Xue, Q., Ding, Y. and Yabuta, K., ‘Parabolic Littlewood–Paley g-function with rough kernel’, Acta Math. Sin. (Engl. Ser.) 24 (2008), 2049–2060.CrossRefGoogle Scholar
Yano, S., ‘An extrapolation theorem’, J. Math. Soc. Japan 3 (1951), 296–305.CrossRefGoogle Scholar