Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T02:45:41.162Z Has data issue: false hasContentIssue false
  • English
  • Français

Local polynomial functions on factor rings of the integers

Published online by Cambridge University Press:  09 April 2009

Hans Lausch  and
Wilfried Nöbauer
Hans Lausch
Affiliation:
Department of MathematicsMonash University Clayton, Vic. 3168, Australia
Wilfried Nöbauer
Affiliation:
Institut für Algebra und Mathematische Strukturtheorie Technische UniversitātArgentinierstrasse 8 A-1040 Wien, Austria
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a universal algebra. A function ϕ Ak-A is called a t-local polynomial function, if ϕ can ve interpolated on any t places of Ak by a polynomial function— for the definition of a polynomial function on A, see Lausch and Nöbauer (1973), Let Pk(A) be the set of the polynomial functions, LkPk(A) the set of all t-local polynmial functions on A and LPk(A) the intersection of all LtPk(A), then 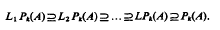. If A is an abelian group, then this chain has at most five distinct members— see Hule and Nöbauer (1977)— and if A is a lattice, then it has at most three distinct members— see Dorninger and Nöbauer (1978). In this paper we show that in the case of commutative rings with identity there does not exist such a bound on the length of the chain and that, in this case, there exist chains of even infinite length.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 27 , Issue 2 , March 1979 , pp. 232 - 238
Copyright
Copyright © Australian Mathematical Society 1979

References

Dorninger, D. and Nöbauer, W. (1978), ‘Local polynomial functions on lattices and universal algebras’, Colloq. Math. (to appear).CrossRefGoogle Scholar
Hule, H. and Nöbauer, W. (1977), ‘Local polynomial functions on universal algebras’, An. Acad. Brasil. Ciênc. 49 (3), 365–372.Google Scholar
Lausch, H. and Nöbauer, W. (1973), Algebra of polynomials (North Holland, Amsterdam and London).Google Scholar
Nöbauer, W. (1955), ‘Gruppen von Restpolynomidearlrestklassen nach Primzahlpotenzen’, Monatsh. Math. 59, 194–202.CrossRefGoogle Scholar