Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-09T15:30:28.658Z Has data issue: false hasContentIssue false
  • English
  • Français

LINEAR MAPS PRESERVING TENSOR PRODUCTS OF RANK-ONE HERMITIAN MATRICES

Part of: Special matrices Basic linear algebra

Published online by Cambridge University Press:  21 November 2014

JINLI XU ,
BAODONG ZHENG  and
AJDA FOŠNER
JINLI XU*
Affiliation:
Department of Mathematics, Harbin Institute of Technology, Harbin 150001, PR China email jclixv@qq.com
BAODONG ZHENG
Affiliation:
Department of Mathematics, Harbin Institute of Technology, Harbin 150001, PR China email zbd@hit.edu.cn
AJDA FOŠNER
Affiliation:
Faculty of Management, University of Primorska, Cankarjeva 5, SI-6104 Koper, Slovenia email ajda.fosner@fm-kp.si
*
✉jclixv@qq.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a positive integer 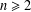$n\geq 2$, let 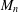$M_{n}$ be the set of 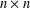$n\times n$ complex matrices and 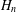$H_{n}$ the set of Hermitian matrices in 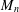$M_{n}$. We characterize injective linear maps 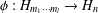${\it\phi}:H_{m_{1}\cdots m_{l}}\rightarrow H_{n}$ satisfying

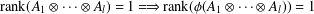$$\begin{eqnarray}\text{rank}(A_{1}\otimes \cdots \otimes A_{l})=1\Longrightarrow \text{rank}({\it\phi}(A_{1}\otimes \cdots \otimes A_{l}))=1\end{eqnarray}$$
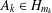for all $A_{k}\in H_{m_{k}}$, 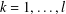$k=1,\dots ,l$, where 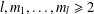$l,m_{1},\dots ,m_{l}\geq 2$ are positive integers. The necessity of the injectivity assumption is shown. Moreover, the connection of the problem to quantum information science is mentioned.

Keywords

quantum information sciencelinear preservertensor productrank-one matrixHermitian matrix

MSC classification

Primary: 15A03: Vector spaces, linear dependence, rank
Secondary: 15A69: Multilinear algebra, tensor products 15A86: Linear preserver problems 15B57: Hermitian, skew-Hermitian, and related matrices
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 3 , June 2015 , pp. 407 - 428
Copyright
© 2014 Australian Mathematical Publishing Association Inc. 

References

Bourbaki, N., Algebra I, Elements of Mathematics, 2 (Springer, New York, 1989).Google Scholar
Chebotar, M. A., Brešar, M. and Martindale, W. S., Functional Identities (Birkhäuser, Basel, 2007).Google Scholar
Gao, X.-Y. and Zhang, X., ‘Additive rank-1 preservers between spaces of Hermitian matrices’, J. Appl. Math. Comput. 26 (2008), 183–199.Google Scholar
Jain, A. K., Fundamentals of Digital Image Processing (Prentice-Hall, Englewood Cliffs, NJ, 1989).Google Scholar
Johnston, N., ‘Characterizing operations preserving separability measures via linear preserver problems’, Linear Multilinear Algebra 59 (2011), 1171–1187.Google Scholar
Li, C.-K., Fošner, A., Huang, Z. and Sze, N.-S., ‘Linear preservers and quantum information science’, Linear Multilinear Algebra 61 (2013), 1377–1390.Google Scholar
Li, C.-K. and Pierce, S., ‘Linear preserver problems’, Amer. Math. Monthly 108 (2001), 591–605.Google Scholar
Mac Lane, S. and Birkhoff, B., Algebra (American Mathematical Society, Providence, RI, 1999).Google Scholar
Molnár, L., Selected Preserver Problems on Algebraic Structures of Linear Operators and on Function Spaces, Lecture Notes in Mathematics, 1895 (Springer, Berlin, 2007).Google Scholar
Nielsen, M. A. and Chuang, I. L., Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, UK, 2000).Google Scholar
Poon, Y.-T., Friedland, S., Li, C.-K. and Sze, N.-S., ‘The automorphism group of separable states in quantum information theory’, J. Math. Phys. 52 (2011), 042203.Google Scholar
Poon, Y.-T., Li, C.-K. and Sze, N.-S., ‘Linear preservers of tensor product of unitary orbits and product numerical range’, Linear Algebra Appl. 438 (2013), 3797–3803.Google Scholar
Steeb, W.-H. and Yorick, H., Matrix Calculus and Kronecker Product: A Practical Approach to Linear and Multilinear Algebra, 2nd edn (World Scientific, Singapore, 2011).Google Scholar
Tang, X.-M., ‘Additive rank-1 preservers between Hermitian matrix spaces and applications’, Linear Algebra Appl. 395 (2005), 333–342.CrossRefGoogle Scholar
Wan, Z.-X., Geometry of Matrices (World Scientific, Singapore, 1996).CrossRefGoogle Scholar
Xu, J.-L., Zheng, B.-D. and Fošner, A., ‘Linear maps preserving rank of tensor products of matrices’, Linear Multilinear Algebra (2014); doi:10.1080/03081087.2013.869589.Google Scholar