Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T23:20:22.656Z Has data issue: false hasContentIssue false
  • English
  • Français

The limiting distribution of a recursive resampling procedure

Part of: Stochastic processes

Published online by Cambridge University Press:  09 April 2009

Zheng Zukang  and
Wu Lipeng
Zheng Zukang
Affiliation:
Department of Statistics and Operations Research, Fudan University, Shanghai, 200433, China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A recursive resampling method is discussed in this paper. Let X1, X2,…, Xn, be i.i.d. random variables with distribution function F and construct the empirical distribution function Fn. A new sample Xn+1 is drawn from Fn and the new empirical distribution function 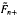1 in the wide sense, is computed from X1, X2,…, Xn, Xn+1. Then Xn+2 is drawn from 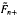1 and 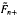2 is obtained. In this way, Xn+m and 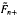m are found. It will be proved that 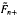m converges to a random variable almost surely as m goes to infinity and the limiting distribution is a compound beta distribution. In comparison with the usual non-recursive bootstrap, the main advantage of this procedure is a reduction in unconditional variance.

MSC classification

Secondary: 60G50: Sums of independent random variables; random walks
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 58 , Issue 1 , February 1995 , pp. 47 - 53
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Chow, Y. S. and Teicher, H., Probability theory (Springer-Verlag, New York, 1978).CrossRefGoogle Scholar
[2]Efron, B., The jackknife, the bootstrap, and other resampling schemes (SIAM, Philadelphia, 1982).Google Scholar
[3]Johnson, N. L. and Kotz, S., Urn models and their application (Wiley, New York, 1977).Google Scholar
[4]Rubin, D. P., ‘The Bayesian bootstrap’, Ann. Statist. 9 (1981), 130–134.CrossRefGoogle Scholar