Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T08:02:47.510Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattic isomorphisms of lie algebras

Published online by Cambridge University Press:  09 April 2009

D. W. Barnes
D. W. Barnes
Affiliation:
Mathamatics Department, University of Sydney.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

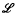Let L be a finite dimensional Lie algebra over the Field F. We denote by (L) the lattice of all subalgebras of L. By a lattice isomorphiusm (whicn we abbrevite to 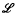-isomorphism) of L onto a Lie algebra M over the same field F, we mean an isomorphism of 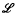(L) onto 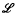(M). It is possible for non-isomorphic Lie algebras to 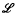-isomorphic, for example, the algebra of real vectors with product the vector product is 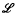-isomorphic to any 2-dimensional Lie algebra over the field of real numbers.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 4 , Issue 4 , November 1964 , pp. 470 - 475
Copyright
Copyright © Australian Mathematical Society 1964

References

[1]Barnes, D. W. and Wall, G. E., On normaliser preserving lattice isomorphisms between nilpotent groups (to appear).Google Scholar
[2]Jacobson, N., Lie algebras, Interscience Tracts No. 10. New York, 1962.Google Scholar
[3]Séminaire, “Sophus Lie”: 1954/55, Théorie des algèbres de Lie, topologie des groupes de Lie (Ecole Normale Supérieure, Paris, 1955).Google Scholar