Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T08:24:52.330Z Has data issue: false hasContentIssue false
  • English
  • Français

THE K-THEORY OF SOME HIGHER RANK EXEL–LACA ALGEBRAS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  01 February 2008

BERNHARD BURGSTALLER
BERNHARD BURGSTALLER*
Affiliation:
Institute of Mathematics, University of Münster, Einsteinstrasse 62, 48149 Münster, Germany (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

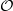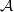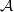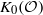Let be a higher rank Exel–Laca algebra generated by an alphabet . If contains d commuting isometries corresponding to rank d and the transition matrices do not have finite rows, then is trivial and is isomorphic to K0 of the abelian subalgebra of 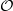generated by the source projections of .

Keywords

K-theoryExel–Laca algebragraph algebrahigher rank

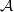MSC classification

Secondary: 46L80: $K$-theory and operator algebras (including cyclic theory) 46L55: Noncommutative dynamical systems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 84 , Issue 1 , February 2008 , pp. 21 - 38
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Allen, S., Pask, D. and Sims, A., ‘A dual graph construction for higher-rank graphs, and K-theory for finite 2-graphs’, Proc. Amer. Math. Soc. 134 (2006), 455–464.CrossRefGoogle Scholar
[2]Bowen, R. and Franks, J., ‘Homology for zero-dimensional nonwandering sets’, Ann. Math. 106 (1977), 73–92.CrossRefGoogle Scholar
[3]Burgstaller, B., ‘An extension of the Cuntz–Krieger type class’, Preprint.Google Scholar
[4]Burgstaller, B., ‘Some multidimensional Cuntz algebras’, Aequationes Math. to appear.Google Scholar
[5]Burgstaller, B., ‘The uniqueness of Cuntz–Krieger type algebras’, J. Reine Angew. Math. 594 (2006), 207–236.Google Scholar
[6]Burgstaller, B., ‘A class of higher rank Exel–Laca algebras’, Acta Sci. Math. 73 (2007), 209–235.Google Scholar
[7]Burgstaller, B. and Evans, G. D., ‘On graph and Cuntz–Krieger type algebras’, Preprint.Google Scholar
[8]Connes, A., ‘An analogue of the Thom isomorphism for crossed products of a C *-algebra by an action of ’, Adv. Math. 39 (1981), 31–55.CrossRefGoogle Scholar
[9]Cuntz, J., ‘A class of C *-algebras and topological Markov chains II: reducible chains and the Ext-functor for C *-algebras’, Invent. Math. 63 (1981), 25–40.CrossRefGoogle Scholar
[10]Cuntz, J., ‘K-theory for certain C *-algebras’, Ann. Math. 113 (1981), 181–197.CrossRefGoogle Scholar
[11]Drinen, D. and Tomforde, M., ‘Computing K-theory and Ext for graph C *-algebras’, Illinois J. Math. 46 (2002), 81–91.CrossRefGoogle Scholar
[12]Evans, D. G., ‘On the K-theory of higher rank graph C *-algebras’, New York J. Math. 14 (2008), 1–31.Google Scholar
[13]Exel, R. and Laca, M., ‘Cuntz–Krieger algebras for infinite matrices’, J. Reine Angew. Math. 512 (1999), 119–172.CrossRefGoogle Scholar
[14]Exel, R. and Laca, M., ‘The K-theory of Cuntz–Krieger algebras for infinite matrices’, K-theory 19 (2000), 251–268.CrossRefGoogle Scholar
[15]Kasparov, G. G., ‘Equivariant KK-theory and the Novikov conjecture’, Invent. Math. 91 (1988), 147–201.CrossRefGoogle Scholar
[16]Katsura, T., ‘A class of C *-algebras generalizing both graph algebras and homeomorphism C *-algebras. I. Fundamental results’, Trans. Amer. Math. Soc. 356 (2004), 4287–4322.CrossRefGoogle Scholar
[17]Kirchberg, E., ‘Michael’s noncommutative selection principle and the classification of nonsimple algebras’, C *-algebras. Proceedings of the SFB-workshop, Münster, Germany, 8–12 March 1999 (eds. J. Cuntz et al.) (Springer, Berlin, 2000), pp. 92–141.CrossRefGoogle Scholar
[18]Kumjian, A. and Pask, D., ‘Higher rank graph C *-algebras’, New York J. Math. 6 (2000), 1–20.Google Scholar
[19]Pask, D. and Raeburn, I., ‘On the K-theory of Cuntz–Krieger algebras’, Publ. Res. Inst. Math. Sci. 32 (1996), 415–443.CrossRefGoogle Scholar
[20]Phillips, N. C., ‘A classification theorem for nuclear purely infinite simple C *-algebras’, Doc. Math., J. DMV 5 (2000), 49–114.CrossRefGoogle Scholar
[21]Pimsner, M. and Voiculescu, D., ‘Exact sequences for K-groups and Ext-groups of certain cross-products C *-algebras’, J. Operator Theory 4 (1980), 93–118.Google Scholar
[22]Popescu, I. and Zacharias, J., ‘E-theoretic duality for higher rank graph algebras’, K-Theory 34 (2005), 265–282.CrossRefGoogle Scholar
[23]Raeburn, I., Sims, A. and Yeend, T., ‘Higher-rank graphs and their C *-algebras’, Proc. Edinb. Math. Soc., II. Ser. 46 (2003), 99–115.CrossRefGoogle Scholar
[24]Raeburn, I., Sims, A. and Yeend, T., ‘The C *-algebras of finitely aligned higher-rank graphs’, J. Funct. Anal. 213 (2004), 206–240.CrossRefGoogle Scholar
[25]Raeburn, I. and Szymański, W., ‘Cuntz–Krieger algebras of infinite graphs and matrices’, Trans. Amer. Math. Soc. 356 (2004), 39–59.CrossRefGoogle Scholar
[26]Rørdam, M., Larsen, F. and Laustsen, N., An introduction to K-theory for C *-algebras, London Mathematical Society Student Texts, 49 (Cambridge University Press, Cambridge, 2000).CrossRefGoogle Scholar
[27]Robertson, G. and Steger, T., ‘C *-algebras arising from group actions on the boundary of a triangle building’, Proc. London Math. Soc. 72 (1996), 613–637.CrossRefGoogle Scholar
[28]Robertson, G. and Steger, T., ‘Affine buildings, tiling systems and higher rank Cuntz–Krieger algebras’, J. Reine Angew. Math. 513 (1999), 115–144.CrossRefGoogle Scholar
[29]Robertson, G. and Steger, T., ‘Asymptotic K-theory for groups acting on buildings’, Canad. J. Math. 53 (2001), 809–833.CrossRefGoogle Scholar
[30]Szymański, W., ‘The range of K-invariants for C *-algebras of infinite graphs’, Indiana Univ. Math. J. 51 (2002), 239–249.CrossRefGoogle Scholar