Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-20T16:27:16.834Z Has data issue: false hasContentIssue false
  • English
  • Français

INVARIANT SUBSPACES IN THE BIDISC AND WANDERING SUBSPACES

Part of: General theory of linear operators Commutative Banach algebras and commutative topological algebras

Published online by Cambridge University Press:  01 June 2008

TAKAHIKO NAKAZI
TAKAHIKO NAKAZI*
Affiliation:
Department of Mathematics, Faculty of Science, Hokkaido University, Sapporo 060-0810, Japan (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be a forward-shift-invariant subspace and N a backward-shift-invariant subspace in the Hardy space H2 on the bidisc. We assume that 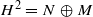. Using the wandering subspace of M and N, we study the relations between M and N. Moreover we study M and N using several natural operators defined by shift operators on H2.

Keywords

invariant subspacetwo variable Hardy spacewandering subspace

MSC classification

Secondary: 47A15: Invariant subspaces 46J15: Banach algebras of differentiable or analytic functions, $H^p$-spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 84 , Issue 3 , June 2008 , pp. 367 - 374
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Beurling, A., ‘On two problems concerning linear transformations in Hilbert space’, Acta Math. 81 (1949), 239–255.CrossRefGoogle Scholar
[2]Ghatage, P. and Mandrekar, V., ‘On Beurling type invariant subspaces of L 2(T 2) and their equivalence’, J. Operator Theory 20 (1988), 31–38.Google Scholar
[3]Guo, K. and Yang, R., ‘The core function of submodules over the bidisk’, Indiana Univ. Math. J. 53 (2004), 205–222.Google Scholar
[4]Izuchi, K. and Nakazi, T., ‘Backward shift invariant subspaces in the bidisc’, Hokkaido Math. J. 3 (2004), 247–254.Google Scholar
[5]Izuchi, K., Nakazi, T. and Seto, M., ‘Backward shift invariant subspaces in the bidisc II’, J. Operator Theory 51 (2004), 361–376.Google Scholar
[6]Mandrekar, V., ‘The validity of Beurling theorems in polydiscs’, Proc. Amer. Math. Soc. 103 (1988), 145–148.Google Scholar
[7]Nakazi, T., ‘Certain invariant subspaces of H 2 and L 2 on a bidisc’, Canad. J. Math. 40 (1988), 1272–1280.Google Scholar
[8]Nakazi, T., ‘Invariant subspaces in the bidisc and commutators’, J. Aust. Math. Soc. 56 (1994), 232–242.Google Scholar
[9]Nakazi, T., ‘Homogeneous polynomials and invariant subspaces in the polydiscs’, Arch. Math. 58 (1992), 56–63.Google Scholar