Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T08:29:31.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant subspace lattices of Lambert's weighted shifts

Part of: Special classes of linear operators Individual linear operators as elements of algebraic systems General theory of linear operators

Published online by Cambridge University Press:  09 April 2009

B. S. Yadav  and
S. Chatterjee
B. S. Yadav
Affiliation:
Department of Mathematics University of DelhiDelhi-110007, India
S. Chatterjee
Affiliation:
Department of Mathematics University of DelhiDelhi-110007, India
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let B(H) be the Banach algebra of all (bounded linear) operators on an infinite-dimensional separable complex Hilbert space H and let 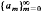be a bounded sequence of positive real numbers. For a given injective operator A in B(H) and a non-zero vector f in H, we put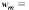 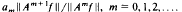We define a weighted shift Tw with the weight sequence 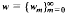on the Hilbert space 12 of all square-summable complex sequences 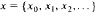by 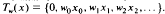. The main object of this paper is to characterize the invariant subspace lattice of Tw under various nice conditions on the operator A and the sequence .

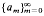MSC classification

Secondary: 47A15: Invariant subspaces 47B99: None of the above, but in this section 47C05: Operators in algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 33 , Issue 1 , August 1982 , pp. 135 - 142
Copyright
Copyright © Australian Mathematical Society 1982

References

1.Donoghue, W. F., ‘The lattice of invariant subspaces of a completely Continuous quasi-nilpotent transformation’, Pacific J. Math. 7 (1957), 1031–1035.CrossRefGoogle Scholar
2.Embry, Mary R., ‘Strictly cyclic operator algebras on a Banach space’, Pacific J. Math. 45 (1973), 443–452.CrossRefGoogle Scholar
3.Halmos, P. R., ‘Ten problems in Hilbert space’, Bull. Amer. Math. Soc. 78 (1970), 887–933.CrossRefGoogle Scholar
4.Harrison, K. J., ‘On the unicellularity of weighted shifts’, J. Austral. Math. Soc. 12 (1971), 342–350.CrossRefGoogle Scholar
5.Kelley, R. L., Weighted shifts on Hubert space (Thesis, University of Michigan, Ann Arbor, Mich., 1966).Google Scholar
6.Lambert, Alan, ‘Subnormality and weighted shifts’, J. London Math Soc. (2) 14 (1976), 476–480.CrossRefGoogle Scholar
7.Nikolskiĩ, N. K., ‘Invariant subspaces of certain completely continuous operators’, Vesinik Leningrad. Univ. Math. (7) 20 (1965), 68–77 (Russian).Google Scholar
8.Nikolskiĩ, N. K., ‘Invariant subspaces of weighted shift operators’, Math. USSR-Sb. 3 (1967), 159–176.CrossRefGoogle Scholar
9.Nikoiskiĩ, N. K., ‘Basiness and unicellularity of weighted shift operators’, Functional Anal. Appl. 2 (1968), 95–98.Google Scholar
10.Nordgren, Eric A., ‘Invariant subspaces of a direct sum of weighted shifts’, Pacific J. Math. 27 (1968), 587–598.CrossRefGoogle Scholar
11.Pervin, William J., Foundations of general topology (Academic Press, New York, 1970).Google Scholar
12.Riesz, F. and Sz.-Nagy, B., Functional analysis (Ungar, New York, 1955).Google Scholar
13.Shields, A., Weighted shift operators and analytic function theory (Mathematical Surveys, No. 13, edited by Pearcy, C., Amer. Math. Soc., Providence, R. I., 1974).CrossRefGoogle Scholar
14.Sz.-Nagy, B. and Foiaş, C., Harmonic analysis of operators on Hilbert space (Akadémiai Kiadó, Budapest, 1970).Google Scholar
15.Zygmund, A., Trigonometric series (Vol. I, 2nd ed., Cambridge Univ. Press, New York, 1959).Google Scholar