Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cunningham, F.
1966.
Generalization of a theorem of P. D. Finch's on integration of set-functions.
Journal of the Australian Mathematical Society,
Vol. 6,
Issue. 4,
p.
460.


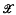 an abstract space of points
an abstract space of points 