Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-02T19:16:46.593Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral operator methods for generalized axially symmetric potentials in (n+1) variables*

Published online by Cambridge University Press:  09 April 2009

R. P. Gilbert  and
H. C. Howard
R. P. Gilbert
Affiliation:
Georgetown University, Washington, D.C.
H. C. Howard
Affiliation:
University of Wisconsin-Milwaukee, Milwaukee, Wisconsin.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall use the integral operator method of Bergman, B[1–6], to investigate solutions of the partial differential equation 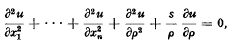where s > −1. In particular, information concerning the growth, and location of singularities, of solutions of (1.1) will be obtained. Equations of the form (1.1) with s = 1, 2, arise from the (n+k+1)-dimensional Laplace equation Δn+k+1u = 0 in the “axially symmetric” coordinates x1, …xn, p where the relationship between cartesian and “axially symmetric” coordinates is given by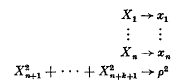

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 5 , Issue 3 , August 1965 , pp. 331 - 348
Copyright
Copyright © Australian Mathematical Society 1965

References

[A de F.1]Appell, P., and de Fériet, J., Fonctions hypergéométriques et hypersphériques, Polynomes d'Hermite, Gauthier-Villars, Paris (1926).Google Scholar
[B.1]Bergman, S.Zur Theorie der ein- und mehrwertigen harmonischen Funktionen des drei dimensional Raumes, Math. Zeit. 24 (1926). 641–669.Google Scholar
[B.2]Bergman, S., Integral operators in the theory of linear partial differential equations, Ergeb. Math. u. Grenzgeb., 23, Springer, Berlin (1960).Google Scholar
[B.3]Bergman, S., Operators generating solutions of certain differential equations in three variables and their properties, Scripta Math., 26 (1961), 5–31.Google Scholar
[B.4]Bergman, S., Some properties of a harmonic function of three variables given by its series development, Arch. Rat. Mech. Anal. 8 (1961), 207–222.Google Scholar
[B.5]Bergman, S., Sur les singularités des fonctions harmoniques de trois variables, Comptes rendus des séances de l'Académie des Sciences 254 (1962), 3482–3483.Google Scholar
[B.6]Bergman, S., Integral operators in the study of an algebra and of a coefficient problem in the theory of three-dimensional harmonic functions, Duke Math. Journal 30 (1963), 447–460.Google Scholar
[B.M.1]Bochner, S., and Martin, W. T., Several Complex Variables, Princeton Math. Series 10, Princeton Univ. Press, Princeton (1948).Google Scholar
[E.1]Erdélyi, A., Singularities of generalized axially symmetric potentials, Comm. Pure Appl. Math. 9 (1956), 403–414.Google Scholar
[E.2]Erdélyi, A., Higher transcendental functionsII, McGraw-Hill, New York (1953).Google Scholar
[F.1]Fuks, B. A., Introduction to the theory of analyticfunctions of several comlex variables. Translations of Mathematical Monographs 8, American Mathematical Society. Providence (1963).Google Scholar
[G.1]Gilbert, R. P., Singularities of three-dimensional harmonic functions, Pac. J. Math. 10 (1961), 1243–1255.Google Scholar
[G.2]Gilbert, R. P., Integral operator methods in bi-axially symmetric potential theory. Contrib. Diff. Equat. Vol. II, No. 3, (1963), 441–456.Google Scholar
[G.3]Gilbert, R. P., Bergman's integral operator method in generalized axially symmetric potential theory, J. of Mathematical Physics, 5, (1964), 983–997.Google Scholar
[G.4]Gilbert, R. P., On harmonic functions of four-variables with rational p4associates, Pacific J. Math., 13 (1963), 79–96.Google Scholar
[G.H.1]Gilbert, R. P. and Howard, H. C., On solutions of the generalized axially symmetric wave equation represented by Bergman operators, Proc. Lond. Math. Soc., 3rd series, XV (2), (1965), 346–360.Google Scholar
[G.H.2]Gilbert, R. P. and Howard, H. C., On solutions of the generalized bi-axially symmetric Helmholtz equation generated by integral operators, J. für reine u. angew. Math. 218 (1965) 109–120.Google Scholar
[H.1]Hadamard, J., Théoréme sur les series entiers, Acta Math. 22 (1898), 55–64.Google Scholar
[H.2]Henrici, P., Zur Funktionen theorie der Wellengleichung, Comm. Math. Helv. 27 (1953), 235–293.CrossRefGoogle Scholar
[H.3]Henrici, P., On the domain of regularity of generalized axially symmetric potentials, Proc. Amer. Math. Soc. 8 (1957), 29–31.Google Scholar
[H.4]Henrici, P., Complete systems of solutions for a class of singular elliptic partial differential equations, Boundary Value Problems in Differential Equations, pp. 19–34, Univ. of Wisconsin (1960).Google Scholar
[W.1]Weinstein, A., Singular partial differential equations and their applications. Proc. Symp. on Fluid Dynamics and Applied Mathematics, Gordon and Breach, New York. (1961).Google Scholar