Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T07:01:54.106Z Has data issue: false hasContentIssue false
  • English
  • Français

IDEALS IN OPERATOR SPACE PROJECTIVE TENSOR PRODUCT OF C*-ALGEBRAS

Part of: Selfadjoint operator algebras Linear spaces and algebras of operators

Published online by Cambridge University Press:  18 November 2011

RANJANA JAIN  and
AJAY KUMAR
RANJANA JAIN
Affiliation:
Department of Mathematics, Lady Shri Ram College for Women, New Delhi-110024, India (email: [email protected])
AJAY KUMAR*
Affiliation:
Department of Mathematics, University of Delhi, Delhi-110007, India (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

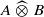Let A and B be C*-algebras. We prove the slice map conjecture for ideals in the operator space projective tensor product . As an application, a characterization of the prime ideals in the Banach *-algebra 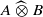is obtained. In addition, we study the primitive ideals, modular ideals and the maximal modular ideals of . We also show that the Banach *-algebra possesses the Wiener property and that, for a subhomogeneous C*-algebra A, the Banach * -algebra is symmetric.

Keywords

C*-algebrasoperator space projective tensor normHaagerup tensor product

MSC classification

Secondary: 46L06: Tensor products of $C^*$-algebras 47L25: Operator spaces (= matricially normed spaces)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 91 , Issue 2 , October 2011 , pp. 275 - 288
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

References

[1]Allen, S. D., Sinclair, A. M. and Smith, R. R., ‘The ideal structure of the Haagerup tensor product of C *-algebras’, J. reine angew. Math. 442 (1993), 111–148.Google Scholar
[2]Archbold, R. J., ‘A counter example for commutation in tensor products of C *-algebras’, Proc. Amer. Math. Soc. 81 (1981), 562–564.Google Scholar
[3]Archbold, R. J., Kaniuth, E., Schlichting, G. and Somerset, D. W. B., ‘Ideal space of the Haagerup tensor product of C *-algebras’, Internat. J. Math. 8 (1997), 1–29.CrossRefGoogle Scholar
[4]Blackadar, B., Operator Algebras—Theory of C *-algebras and von-Neumann Algebras (Springer, Berlin–Heidelberg–New York, 2006).Google Scholar
[5]Blecher, D. P. and LeMerdy, C., ‘On quotients of function algebras and operator algebra structures on l p’, J. Operator Theory 34 (1995), 315–346.Google Scholar
[6]Blecher, D. P. and Paulsen, V. I., ‘Tensor products of operator spaces’, J. Funct. Anal. 99 (1991), 262–292.CrossRefGoogle Scholar
[7]Bonic, R. A., ‘Symmetry in group algebras of discrete groups’, Pacific J. Math 11 (1961), 73–94.CrossRefGoogle Scholar
[8]Effros, E. G. and Ruan, Z. J., ‘On matricially normed spaces’, Pacific J. Math. 132 (1988), 243–264.CrossRefGoogle Scholar
[9]Effros, E. G. and Ruan, Z. J., ‘A new approach to operator space’, Canad. Math. Bull. 34 (1991), 329–337.CrossRefGoogle Scholar
[10]Hauenschild, W., Kaniuth, E. and Kumar, A., ‘Ideal structure of Beurling algebras on [FC]− groups’, J. Funct. Anal. 51 (1983), 213–228.CrossRefGoogle Scholar
[11]Jain, R. and Kumar, A., ‘Operator space tensor products of C *-algebras’, Math. Z. 260 (2008), 805–811.CrossRefGoogle Scholar
[12]Jain, R. and Kumar, A., ‘Operator space projective tensor product: embedding into second dual and ideal structure’, arXiv:1106.2644v1 [math.OA].Google Scholar
[13]Kaniuth, E., A Course in Commutative Banach Algebras (Springer, New York, 2009).CrossRefGoogle Scholar
[14]Kumar, A., ‘Operator space projective tensor product of C *-algebras’, Math. Z. 237 (2001), 211–217.CrossRefGoogle Scholar
[15]Kumar, A. and Sinclair, A. M., ‘Equivalence of norms on operator space tensor products of C *-algebras’, Trans. Amer. Math. Soc. 350 (1998), 2033–2048.CrossRefGoogle Scholar
[16]Lebow, A., ‘Maximal ideals in tensor products of Banach algebras’, Bull. Amer. Math. Soc. 74 (1968), 1020–1022.CrossRefGoogle Scholar
[17]Leptin, H. and Poguntke, D., ‘Symmetry and nonsymmetry for locally compact groups’, J. Funct. Anal. 33 (1979), 119–134.CrossRefGoogle Scholar
[18]Loy, R. J., ‘Identities in tensor products of Banach algebras’, Bull. Aust. Math. Soc. 2 (1970), 253–260.CrossRefGoogle Scholar
[19]Ludwig, J., ‘A class of symmetric and a class of Wiener group algebras’, J. Funct. Anal. 31 (1979), 187–194.CrossRefGoogle Scholar
[20]Palmer, T. W., Banach Algebras and the General Theory of *-Algebras II (Cambridge University Press, Cambridge, 2001).CrossRefGoogle Scholar
[21]Smith, R. R., ‘Completely bounded module maps and the Haagerup tensor product’, J. Funct. Anal. 102 (1991), 156–175.CrossRefGoogle Scholar
[22]Takesaki, M., Theory of Operator Algebras I, 2nd Printing (Springer, Berlin–Heidelberg–New York, 2002).Google Scholar
[23]Tomiyama, J., ‘Applications of Fubini type theorem to the tensor products of C *-algebras’, Tohoku Math J. 19 (1967), 213–226.CrossRefGoogle Scholar
[24]Wassermann, S., ‘The slice map problem for C *-algebras’, Proc. Lond. Math. Soc. 32 (1976), 537–559.CrossRefGoogle Scholar
[25]Wassermann, S., ‘On tensor products of certain group C *-algebras’, J. Funct. Anal. 23 (1976), 239–254.CrossRefGoogle Scholar