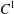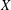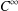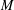Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lee, Seunghee
and
Park, Junmi
2016.
Expansive homoclinic classes of generic C 1-vector fields.
Acta Mathematica Sinica, English Series,
Vol. 32,
Issue. 12,
p.
1451.
Lee, Manseob
2019.
Continuum-wise expansive homoclinic classes for robust dynamical systems.
Advances in Difference Equations,
Vol. 2019,
Issue. 1,
Lee, Manseob
2020.
Robustly measure expansiveness for C1 vector fields.
Quaestiones Mathematicae,
Vol. 43,
Issue. 4,
p.
569.