Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liang, Yu-Xia
and
Zhou, Ze-Hua
2019.
The Nonlinear Superposition Operators Between Zygmund-Type and Bloch-Type Spaces.
Mediterranean Journal of Mathematics,
Vol. 16,
Issue. 2,
Malavé-Malavé, Renny J.
and
Ramos-Fernández, Julio C.
2019.
Superposition operators between logarithmic Bloch spaces.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 68,
Issue. 1,
p.
105.
Domínguez, Salvador
and
Girela, Daniel
2019.
Sequences of zeros of analytic function spaces and weighted superposition operators.
Monatshefte für Mathematik,
Vol. 190,
Issue. 4,
p.
725.
Domínguez, Salvador
and
Girela, Daniel
2020.
A Radial Integrability Result Concerning Bounded Functions in Analytic Besov Spaces with Applications.
Results in Mathematics,
Vol. 75,
Issue. 2,
Malavé-Malavé, Renny J.
and
Ramos-Fernández, Julio C.
2020.
The Integral Weight and Superposition Operators Between Bloch-Type Spaces.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 43,
Issue. 4,
p.
3035.
Domínguez, Salvador
and
Girela, Daniel
2021.
Superposition operators between mixed norm spaces of analytic functions.
Mediterranean Journal of Mathematics,
Vol. 18,
Issue. 1,
Bonet, José
2022.
Weighted Banach spaces of analytic functions with sup-norms and operators between them: a survey.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 116,
Issue. 4,
Tang, Pengcheng
2023.
Superposition operators between normal weight bloch spaces.
Monatshefte für Mathematik,
Vol. 202,
Issue. 3,
p.
637.
Chen, Jiale
Guo, Xin
and
Wang, Maofa
2025.
Littlewood-type theorems for random Dirichlet series.
Science China Mathematics,
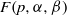 $F(p, \alpha , \beta )$ spaces of Zhao. Some independent properties on these spaces are also obtained.
$F(p, \alpha , \beta )$ spaces of Zhao. Some independent properties on these spaces are also obtained.