Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T08:37:54.873Z Has data issue: false hasContentIssue false
  • English
  • Français

GRASSMANNIAN SEMIGROUPS AND THEIR REPRESENTATIONS

Part of: Special varieties Semigroups Algebraic combinatorics Basic linear algebra Representation theory of rings and algebras

Published online by Cambridge University Press:  27 March 2018

VICTOR CAMILLO  and
MIODRAG C. IOVANOV
VICTOR CAMILLO*
Affiliation:
University of Iowa, MacLean Hall, Iowa City, IA 52246, USA email [email protected]
MIODRAG C. IOVANOV
Affiliation:
University of Iowa, MacLean Hall, Iowa City, IA 52246, USA email [email protected], [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The set of row reduced matrices (and of echelon form matrices) is closed under multiplication. We show that any system of representatives for the 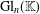$\text{Gl}_{n}(\mathbb{K})$ action on the 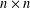$n\times n$ matrices, which is closed under multiplication, is necessarily conjugate to one that is in simultaneous echelon form. We call such closed representative systems Grassmannian semigroups. We study internal properties of such Grassmannian semigroups and show that they are algebraic semigroups and admit gradings by the finite semigroup of partial order preserving permutations, with components that are naturally in one–one correspondence with the Schubert cells of the total Grassmannian. We show that there are infinitely many isomorphism types of such semigroups in general, and two such semigroups are isomorphic exactly when they are semiconjugate in 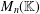$M_{n}(\mathbb{K})$. We also investigate their representation theory over an arbitrary field, and other connections with multiplicative structures on Grassmannians and Young diagrams.

Keywords

semigroupGrassmanniansimultaneous formechelon formrepresentations

MSC classification

Primary: 15A30: Algebraic systems of matrices 20M20: Semigroups of transformations, etc. 14M15: Grassmannians, Schubert varieties, flag manifolds
Secondary: 16G99: None of the above, but in this section 05E99: None of the above, but in this section 20M30: Representation of semigroups; actions of semigroups on sets
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 104 , Issue 3 , June 2018 , pp. 308 - 337
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Camillo, V., ‘Row reduced matrices and annihilator semigroups’, Comm. Algebra 25(6) (1997), 1767–1782.Google Scholar
Chen, J., Khurana, D., Lam, T.-Y. and Wang, Z., ‘Rings of idempotent stable range one’, Algebr. Represent. Theory 15 (2012), 195–200.Google Scholar
Ganyushkin, O. and Mazorchuk, V., Classical Finite Transformation Groups. An Introduction, Algebra and Applications, 9 (Springer, London, 2009).Google Scholar
Grover, H. K., Wang, Z., Khurana, D., Chen, J. and Lam, T. Y., ‘Sums of unit in rings’, J. Algebra Appl. 13(1) (2014), 1350072.Google Scholar
Guralnick, R. M., ‘Triangularization of sets of matrices’, Linear Multilinear Algebra, 9 (1980), 133–140.Google Scholar
Guralnick, R. M., ‘A note on commuting pairs of matrices’, Linear Multilinear Algebra 31 (1992), 71–75.Google Scholar
Howie, J. M., Fundamentals of Semigroup Theory, LMS Monographs, 12 (Clarendon Press, Oxford, 1995), 351.Google Scholar
Khurana, D. and Lam, T.-Y., ‘Clean matrices and unit-regular matrices’, J. Algebra 280(2) (2004), 683–698.Google Scholar
Knuth, D., ‘Permutations, matrices and generalized Young tableaux’, Pacific J. Math. 34 (1970), 709–727.Google Scholar
Leroux, P., Algèbre linéaire: une approache matricielle (Modulo Editeur, Montreal, 1983), 500.Google Scholar
Leroux, P., ‘Reduced matrices and q-log-concavity properties of q-Stirling numbers’, J. Combin. Theory A 54 (1990), 64–84.Google Scholar
Okninski, J., ‘Triangularizable semigroups of matrices’, Linear Algebra Appl. 262 (1997), 111–118.Google Scholar
Okninski, J., Semigroups of Matrices (World Scientific, Singapore, 1998).Google Scholar
Okninski, J. and Putcha, M. S., ‘Semigroup algebras of linear semigroups’, J. Algebra 151 (1992), 304–321.Google Scholar
Putcha, M. S., ‘Linear algebraic semigroups’, Semigroup Forum 22(1) (1981), 287–309.Google Scholar
Radjavi, H. and Rosenthal, P., Simultaneous Triangularization, Universitext (Springer, New York, 2000).Google Scholar
Renner, L. E., ‘Linear algebraic monoids’, Invariant Theory and Algebraic Transformation Groups V, Encyclopedia of Mathematical Sciences, 134 (Springer, Berlin, 2005).Google Scholar