Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T07:25:42.430Z Has data issue: false hasContentIssue false
  • English
  • Français

Generlized Fredholm transformations

Part of: General theory of linear operators

Published online by Cambridge University Press:  09 April 2009

D. G. Tacon
D. G. Tacon
Affiliation:
University of New South WalesP.O. Box 1 Kensington, N.S.W. 2033, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In an earlier paper we showed that the set ψ+ (X, Y) of super Tauberian transformations between two Banach spaces X and Y forms an open subset of B(X, Y) which is closed under perturbation by super weakly compact transformations. In this note we characterize a class dual to ψ+ (X, Y) which we denote by ψ-(X, Y). We show that T∈ψ+(X, Y) if and only if T′ ∈ ψ-(Y′, X′) and that T′∈ψ+(Y′, X′) if and only if T ∈ ψ-(X, Y) and provide standard and nonstandard characterizations of elements of ψ-(X, Y). These two classes thus play in some ways analogous roles to the sets of semi-Fredholm transforms ϕ+ (X, Y) and ϕ-(X, Y).

Moreover 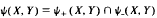en forms an open subset of B(X, Y) closed under the taking of adjoints, under the taking of nonstandard hull extensions, and under perturbation by super weakly compact transformations.

MSC classification

Secondary: 47A53: (Semi-) Fredholm operators; index theories
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 37 , Issue 1 , August 1984 , pp. 89 - 97
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Brown, A. L. and Page, A., Elements of functional analysis (Van Nostrand Reinhold, London, 1970).Google Scholar
[2]Dunford, N. and Schwartz, J. T., Linear operators, Part I (Interscience, New York, 1958).Google Scholar
[3]Henson, C. W. and Moore, L. C. Jr, ‘The nonstandard theory of topological vector spaces,’ Trans. Amer. Math. Soc. 172 (1972), 405–435;CrossRefGoogle Scholar
Erratum, Trans. Amer. Math. Soc. 184 (1973), 509.Google Scholar
[4]Henson, C. Ward, ‘When do two Banach spaces have isometrically isomorphic nonstandard hulls?,’ Israel J. Math. 22 (1975), 57–67.CrossRefGoogle Scholar
[5]Henson, C. Ward, ‘Nonstandard hulls of Banach spaces,’ Israel J. Math. 25 (1976), 108–144.CrossRefGoogle Scholar
[6]James, R. C., ‘Weakly compact sets,’ Trans. Amer. Math. Soc. 113 (1964), 129–140.CrossRefGoogle Scholar
[7]Kalton, N. and Wilansky, A., ‘Tauberian operators on Banach spaces’, Proc. Amer. Math. Soc. 57 (1976), 251–255.Google Scholar
[8]Tacon, D. G., ‘Generalized semi-Fredhoim transformations,’ J. A ustral. Math. Soc., to appear.Google Scholar
[9]Wilansky, A., Functional analysis (Blaisdell, New York, 1964).Google Scholar
[10]Yang, K.-W., ‘The generalized Fredholm operators,’ Trans. Amer. Math. Soc. 216 (1976), 313–326.Google Scholar